引言
卡米诺·西特（Camillo Sitte）在其经典著作《城市建设艺术》中关注并讨论了城市街区和开放空间等微观层面上的美学秩序[1]。他所主张的建设艺术是关于人类建成环境中那些诱人特质的探索与实践，应具备足以忽略地理或文化差异的普遍性。这一系列主张自1889 年提出以来至今仍有不少讨论。一方面，西特的追随者如吉伯德（Gibberd）最早认为人们无须透过抽象的理论来理解中世纪城镇之美，因它惯以人的尺度为参照[2]；另一位追随者莫廷（Moughtin）则试图将那些建筑和广场的美学规律延伸至城市设计和规划的领域[3]；再如克里尔（Krier）在继承了西特关于空间形态控制原则的同时，又希望撇开主观审美经验来客观地理解城市空间[4]。另一方面，现代主义的拥趸们认为这些美学形式仅仅是一个个无法归纳的偶然结果，故应当采用诸如笔直的轴线这类更为工业化、参数化的模式来决定城市物质形态[5]。然而这些僵硬的做法又于理论层面上遭到了后现代主义者所提倡的个体、自主、多元的美学观点的对抗[6]。信息化时代到来后，新的理念和技术开始发挥实际作用。例如：基于“城市信息模型”的数字城市的构建等，为城市设计提供了可视化三维空间方案实验层面的支持[7-8]。
尽管上述诸多观念各有侧重，但如何客观、全面地理解城市空间之美始终是它们共同的话题。其中，狭义的“尺度”是考察空间特征的重要依据，它不仅是物理或几何学上的概念，还具有人类和社会属性[9]。但如今，尺度在工程技术引领下的大量城市建设中已越过了它传统的美学功能，投向了经济和效率的运算。城市建设正在丢失构建物质空间艺术的自觉，而与尺度相关的研究应重新获得重视。尤其是对空间尺度美学的认识，以往的工作多局限于各种具体的基于形状、大小或比例的经验性罗列，缺乏对这些尺度关系构建的美学规律的探究，而未能在诸多琐碎的艺术原则与整体的空间系统之间建立联系，也未能令它在城市建设的中观和宏观层面得到应有的关注。
20 世纪以来的城市公共空间的衰败[10]、空间结构的“没落”[11]，以及“反城市”产物盛行[12]等遗留问题仍是今天城市复兴和未来发展的一大挑战。在现今的数字智慧城市的大背景下，我国正在城市的认知和实践领域探索着一条有别于欧美的城市更新道路。在以人为本的大方向上，针对城市空间艺术规律的探寻也开始更紧密地与城市居民的空间感知相联系[13]。而不管是西特及其追随者，还是反对者们所表述的诸类概念和原则，仍多依赖于自然语言构建的描述、比喻和修辞，有着不可避免的多义性和模糊性[14]，难以在新的语境下发挥作用。以上历史背景和挑战给了我们充分的动机去探索新的方法或视角来重新解读那些看似陈旧观点背后的原理，以唤回被淡忘已久的城市建设艺术，并赋予其新的意义。
1 艺术原则中的空间尺度特征
本文聚焦于探索一种新的描述和解释方法，因此需要回顾过去城市建设艺术思想中那些与空间尺度相关，且在理论和实践层面均被广泛认可的原则，并围绕空间尺度提出恰当的检测对象和分析方法。
1.1 尺度艺术理论化的困境
根据西特、莫廷、萨林加罗斯（Salingaros）[15]、盖尔（Gehl）[16]、萨拉特（Salat）[17]等学者的归纳，一个遵循艺术原则的城市在空间尺度上应至少具备以下条件。
a.尺度的多样性和连续性：以人性化尺度为依据，与人的身体、感知和移动等活动相关的不同尺度之间的协作（包括相互作用、关联和衔接）构成具有自然尺度层级的空间系统，组织为易于辨认（具可读性）的整体。
b.不同尺度空间的分布特征：其分布形式应遵循幂律，即存在极少的大尺度、较少的中间尺度和大量的小尺度要素。
c.大尺度空间的形态特征与地理关系：大尺度空间多为广场型（长宽比不大于3）的社会活动中心且彼此联系比较松散①此外还有尺度数值之间的若干比例关系，因它们是无量纲的，故不在此研究范围内。。
不难发现，上述美学原则并不涉及具体的视觉艺术形式或手法，而是与人们在城市开放空间中的感知和活动密切相关。尽管实践表明空间尺度结构特征能积极并显著地影响空间审美体验的塑造[18]，但必须承认，这些经验性的原则给出的描述十分模糊（例如条件a 中的“协作”“自然”“易于辨认”等），也尚无公认的程序或方法来确定这些尺度所对应的测量对象（例如条件b 没能明确那些尺度“要素”具体的指代，也不明确其“大小”是相对的还是绝对的）[19]。可见，造成该困境的原因在于缺少一个将空间尺度与美学联系起来的清晰、客观、可测的对象。
1.2 凸空间、凸形和凸空间系统
据此，本研究试以凸空间（convex space）②凸空间是凸多边形（convex polygon）在空间感知上的具体形式。凸多边形简称凸形，可被定义为连接任意两个顶点的线段都在该图形内部或边上的多边形。为研究对象，将其用作联系尺度与美学的中介，以更好地解读那些遵循艺术原则的城市空间的尺度特征与规律。在城市开放空间的语境中，凸空间是视觉经验的映射，而视觉经验是人类社交和审美活动的基础。凸空间能将物质环境和人类活动充分联系起来。在视平面上，它们是构成“珠环状”[20]的城市袋形界面[10]；从建筑角度来说，它们是建筑物凹处的“阴角空间”[21]；站在使用者的立场，这些“凹洞”是积极的口袋空间[22]。在拉斯姆森（Rasmussen）看来，相比结构，“洞穴”（cavity）一词更能指明人们建造的目的[23]，而凸空间正是这种洞穴感的具体形式。可见，尽管名称不同，这类空间早已被广泛地察知了。
凸形是凸空间在平面几何上的表达。由建筑实体和开放空间构成的“图—底”（figure-ground）关系平面图是承接此类空间分析的重要技术工具[24]。希利尔和汉森（Hillier &Hanson）最先在凸形与人类社会活动之间建立起了量化联系[20]。在他们的论述中，凸空间尤指图—底平面中呈现为凸形的一系列开放空间。人的视域为不透明的建筑立面所限定，同时也会受到建筑边界延长线的暗示。凸空间的那些明示或暗示的边界使其拥有清晰可辨的尺度。例如威尼斯圣马可广场，尽管并不封闭，但往往会被视为一个存在明确边界、形状和大小的独立空间。将这种认知逻辑运用至城市的整个开放空间，相当于按一定规则将开放空间分解为一组凸空间的过程。那么，该空间即可由这些凸空间及其系统来完成从局部到整体的解析。
1.3 凸空间与人类活动
凸空间是人们在城市界面获取大量信息的一种显著空间特征。光学和声学原理决定了由建筑围合而成的凹形边界能使建筑最大化地向人们传递信息，而这些信息的复杂性和组织性能显著地影响人们的精神状态[25]。由此界定的户外空间在平面上呈现为凸形。换言之，城市户外凸空间能为人们的视听提供较多可访问的、有意义的信息。不仅如此，身处于同一个凸空间的人们也能通过行为、事件交流彼此的信息，且他们也更容易被来自凹形界面的“街道眼”观察到，从而激发更多的信息连接[19]。这有助于人们高效地评估周围的环境，减少外界带来的压力，提升安全感和舒适性[26]，而这正是人们投入审美活动的前提[27]。
此类空间特征常见于西特提出的艺术原则之中。例如公共广场的中心空敞、封闭性、隐藏尖角等要求，都暗示了凸空间的构成要领。不过由于西特未能构建起凸空间或类似的概念，他也就错失了从整体角度归纳和理解这些特征的可能[28]。人们对整体形状的识别有助于空间上的定位，而对细节的准确把握能更好地识别总体的结构[29]，因此从局部到整体的感知体验是相互依存的。这些由建筑界定的户外空间的大小、形状、密度、多样性和连续性等特征是人们理解整体环境的重要信息来源，对人的体验、意象和记忆有十分显著的影响[30-31]。尤其当这些事物的尺度相互关联时，人们更容易保持对它们的记忆，从而铸就心理归属的基础[32]。
因此，凸空间系统可以看作空间感知、体验和理解的映射，它们的尺度和组织方式与人们的各种规模和内容的日常活动密切相关。那么，研究结合前文的论述提出如下假设：凸空间及其系统能有效地解析历史上学者总结的城市开放空间建设艺术的尺度规律，同时揭示近现代城市规划设计中存在的空间尺度问题。
2 测量、分析与统计方法
为验证该假设，研究需要将图—底平面所呈现的开放空间分解为一组凸形，并统计和分析这些凸形的尺度特征，检查这些特征是否能用于解析前文所总结的经验性尺度原则。在此基础上，研究分析和对照两组案例，以揭示各组凸形的尺度及其组织方式在不同组别中的特征。
2.1 凸空间的划分方法
本研究按“最大面积凸形”这一原则来构建凸空间系统，即按面积从大到小依次从开放空间平面中将凸形识别、提取并记录下来，理由如下。
第一，该途径源自希利尔和汉森的“最大体型且最少数量凸形”分解方法[20]。虽然这两个条件时常无法并存[33]，但仍有学者务实地遵照该方法①该方法包含了不少主观判断成分。完成了不少研究[34-35]。这说明将开放空间转换为一组凸形的基本思路是正确且值得借鉴的。以某场地的图—底平面（图1a）为例，图1b 和1c 分别显示了据“最大体型且最少数量”原则划分得到的简略的和较精确的两个凸空间系统。然而，当将凸形的尺度作为统计和分析对象时，该方法往往不能得出可信的结果。因为它的缺陷不仅在于两个条件潜在的冲突，还在于缺少对“体型”的定义——在以往研究中，它可指凸形的面积大小，但更多指其形状的“肥大程度”（fatness），即凸空间在平面互相垂直的两个方向上最大延伸距离之积。冲突的原则和模糊的定义影响了该划分逻辑的一致性，并最终影响到统计的可靠性。
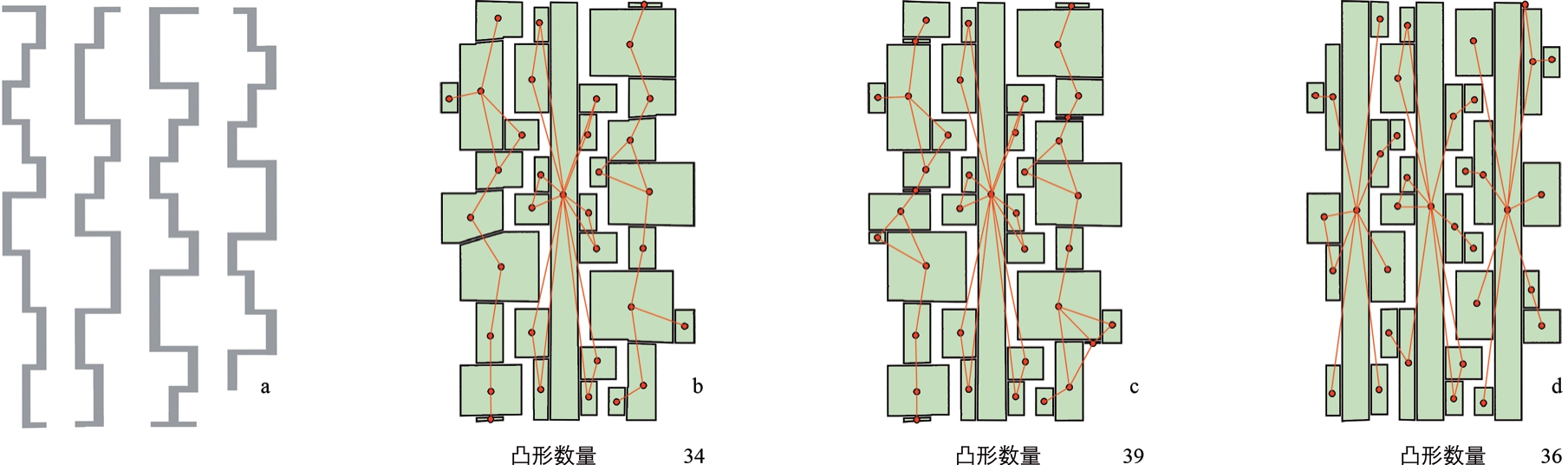
图1 凸空间系统构建方法比较
注：a 图—底平面；b、c 分别为按“最大体型且最少数量”原则划分的简略和较精确凸空间系统；d 为按“最大面积”原则划分的一组凸形
第二，“最大面积凸形”的分解方法很好地再现了人类活动对开放空间的占据方式，反映了人们尽可能地占据更大体量空间的倾向[36]。据前文所述，凸空间中的任意一处对身处其中任意一人都是可见的，那么所谓“占据更大的凸空间”意味着人与人、人与建筑立面、人与事件之间能建立起更多基于相互可视（intervisibility）的信息连接。
第三，由此法分解而来的凸空间数量、几何特征和相互关系反映了身处其中的居民对这些空间及其界面所具有的不同内容、形式和联系的潜在认识和掌控，此类真实或想象的活动和感受建构了主体经验，与第二点一同构成了空间审美最基本的方式[37]。例如：相较于图1b 和1c，图1d 按“最大面积”原则划分的一组凸形更接近人们对该场地空间的真实掌握情况：由轴线主导构成的空间关系在感知上要强于由一系列院落组成的空间序列。
最后也是最重要的，因为在测量中不会得到完全等大的凸形，那么不依赖主观判断的“最大面积”的分解方法便能生成唯一且确定的一组凸形。综上，当研究试用空间尺度特征来解析经验性描述时，该方法在凸空间系统建构的合理性和服务于统计分析的可靠性上均优于“最大体型且最少数量”的划分方法。
2.2 凸空间系统的构建
根据图—底平面图像数据，以直径800 m 的圆形①该范围大小被广泛应用于步行环境的研究，它符合人们适宜的步行距离，而步行则是城市空间美学最重要的感知方式，详见参考文献[3,26]。划定研究范围，并将全部或部分处在研究范围内的所有代表开放空间的连续图形称为g 型图（图2）。凸空间系统的构建就是通过依次识别并提取最大面积凸形，将g 型图分解为一组凸形。这些潜在凸形的所有边都必须落在g 型图的边或边的延长线上，并且忽略面积小于1m2 的凸形以消除资料来源的测量精度对统计的影响。换言之，g 型图等同于去除了建筑及室内空间，且仅取建筑和地形（如水体、山体等障碍）边界及其延长线所能界定的有限面积的开放空间平面。值得注意的是，多数城市并不具备诸如城墙之类的封闭边界，因此要考虑统计全部或部分处在划定范围内且由地图数据给予充分支持的凸形。位于边缘的凸形向外延伸的部分是由范围外部建筑或地形边界来确定的。若有凸形因地图数据不足而趋向于无穷大，则将其排除出统计。
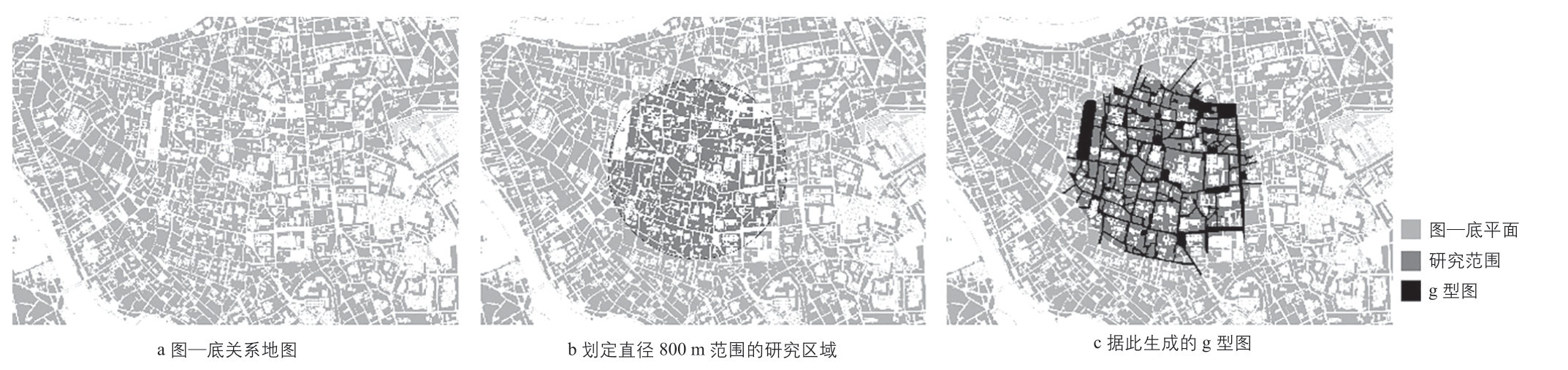
图2 g 型图及研究范围示例
在确定了研究范围后，该系统的构建按如下步骤执行（图3）：
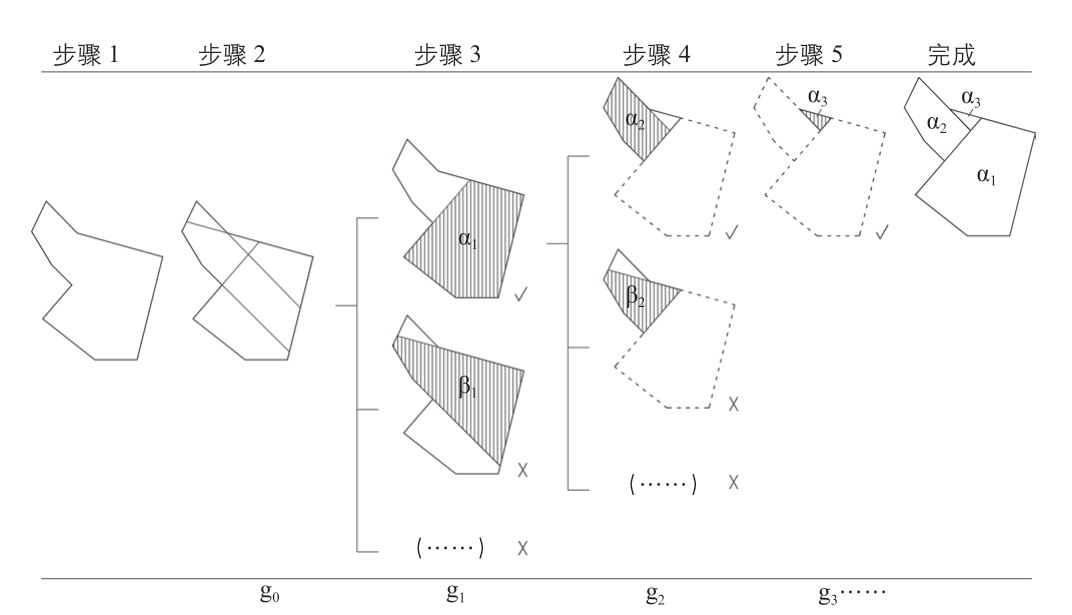
图3 最大凸形提取步骤示例
（1）根据范围内的图—底平面绘制g 型图；
（2）延长g 型图的所有边线至其他边线上，获得图g0，并识别由这些线段构成的所有凸形；
（3）比较图g0 中所有凸形的大小，识别其中面积最大的凸形记为α1，同时获得图g1；
（4）剔除图g1 中的凸形α1 后，识别剩余所有凸形中面积最大凸形记为α2，获得新的图g2；
（5）以此类推，直至剩下唯一的一个不小于1 m2 的凸形αn。
最后，记录面积从大到小的凸形序列（α1,α2,α3…αn）及其平面位置以用于之后的统计、分析、解读和比较。根据1.1小节中整理的艺术原则，研究将着重分析凸形的数量与面积数据之间的关系，以及它们在地理空间上的分布情况。
尽管该方法有明显的合理性和可靠性，但会不可避免地产生诸如图3“步骤5”所示的主要由边界延长线构成的凸形α3，此类凸形与实际感知不符。诸如α3 的存在可视为该方法的缺陷，但必须指出，它事实上也蕴含了某些重要的信息，即作为对g 型图的不规则形式的一种回应。这将在后文中结合具体的案例予以阐明。
2.3 案例选择与依据
研究选取了意大利城市罗马（1748 年）、佛罗伦萨（约1830 年）和英国剑桥（约1800 年）的历史地图，以及美国芝加哥（1909 年）[38]、比利时安特卫普（1933 年）[39]和巴西首都巴西利亚（1956 年）[40]规划的图—底平面为主要案例。其中，前三者作为自下而上发展而来的欧洲传统不规则城市的范型，其历史平面能充分反映西特等人关于城市建设艺术的一系列主张；作为对照的后三者则代表了西特乃至后现代主义者所抨击的“现代体系”，被认为是缺乏艺术价值的产物[41]。
一方面，在形式上符合建设艺术原则的范型城市不胜枚举，而18—19 世纪的罗马、佛罗伦萨和剑桥对本次研究而言更具代表性。首先，它们核心区域的开放空间形态至今仍备受关注，历经广泛的学术讨论且有着丰富的文献资料，充分地呈现了一类未经规划、有机演变的典型结果[42]。其次，历史上这三者在政治、经济、文化的发展定位上各有侧重，从而减小了案例城市的功能定位作为一种额外变量对尺度艺术解读的影响。再次，三者相比其他范型城市（如威尼斯、苏黎世、汉堡等）受地理环境限制较小，有着理论上更自主可控的建设艺术成果。
另一方面，对照案例作为理解城市物质环境的一类重要手段[43]也引入了分析，它们是规划历史上极具代表性的三个作品：奥斯曼影响下的“城市美化运动”中由伯纳姆（Burnham）主导完成的芝加哥规划，现代规划史上的新城代表作——勒·柯布西耶等人规划的安特卫普，以及由科斯塔（Costa）主导完成并被列入“世界文化遗产”的巴西利亚规划。它们完成于不同的历史阶段，有着不一样的空间形态和不同程度的执行结果，因而能更全面地代表“蓝图式”规划思想与前三者进行对照。必须承认，此类规划图在制图精度上与历史地图并不一致。不过，就本文主旨而言，后者所未曾考虑的细节信息及其所强调的理性秩序，正是那些受经验性描述关注、批评，却仍有待阐明的部分，也是后面的分析所要揭示的重要内容之一。
在研究范围的划定中，为了使分析对象具有可比性，将社会活动的核心场所——城市中心区域作为首选范围。当城市存在多个中心或中心范围过大时，所选区域应包含该城市的典型空间结构，同时尽可能体现其多样化的开放空间形态，以减小某些特殊的空间结构（例如码头、自然绿地、城墙、高架桥等）对比较分析的影响。据此，研究以800 m 为直径的圆覆盖上述范围作为各案例城市的研究区域，其图—底平面及其构建的凸空间系统如图4 所示。
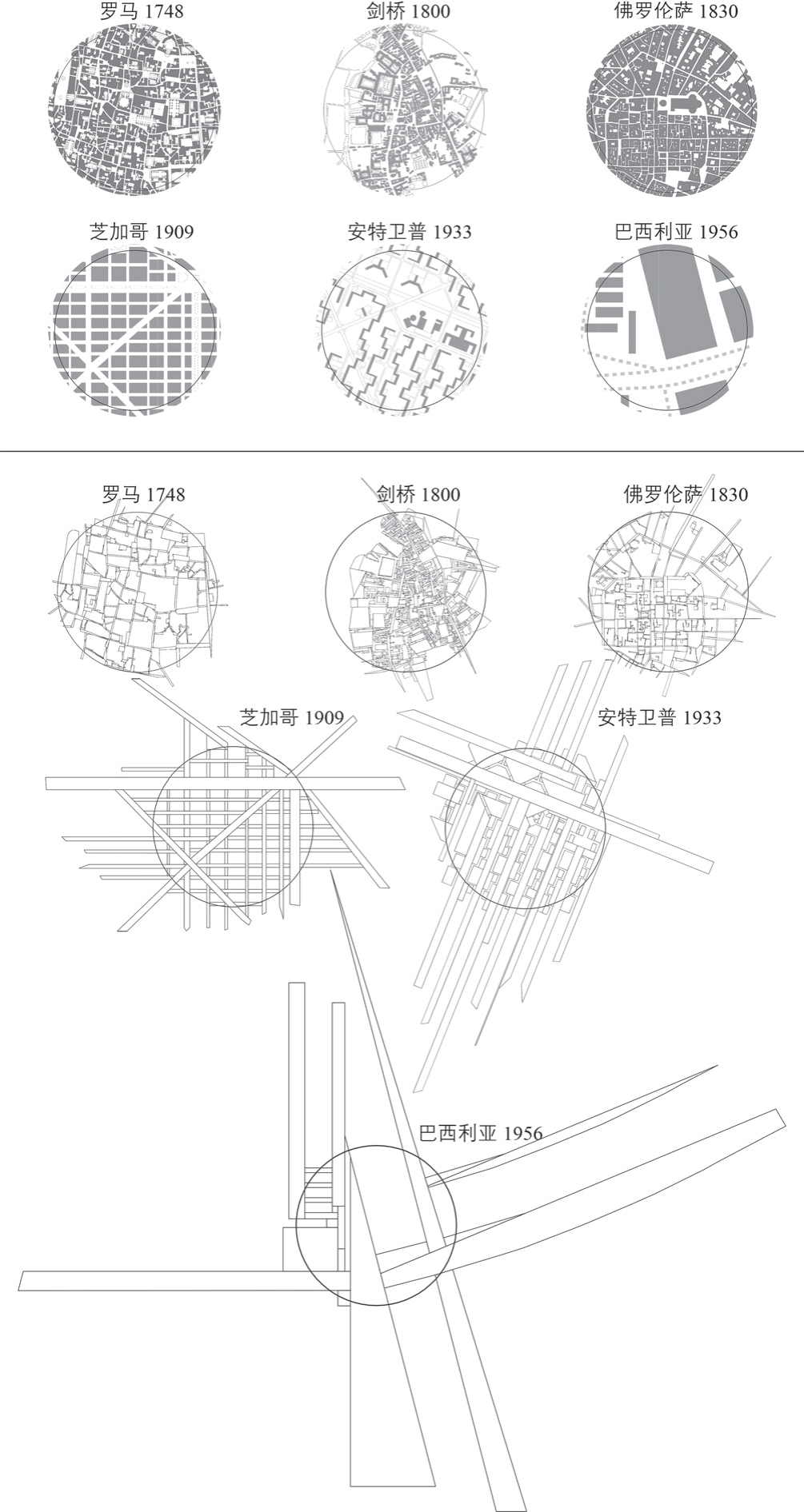
图4 研究区域的图—底平面（上）和据此生成的凸空间系统（下）
资料来源：罗马地图来自https://www.lib.berkeley.edu/EART/maps/nolli_06.jpg，剑桥地图来自https://www.camantsoc.org/19th_century_maps_cambridgeshire/，佛罗伦萨地图来自https://iiif.lib.harvard.edu/manifests/view/ids:9538202，芝加哥、安特卫普和巴西利亚的地图依次来自参考文献[38-40]
3 分析方法、过程与结果
分析由两部分组成，包括对凸空间系统的定性解读和对凸形数量和面积统计数据规律的定量描述，进而完成对研究假设的验证。在定性解读方面，分析将提取各区域中对应于1.1 中“条件c”所述的一组最大的凸形，检查它们的形状和地理分布情况。在定量描述上，分析采用了凸形面积、数量、排名—大小（rank-size，下称r-s）分布以及偏态分布的相关结果。首先，1.1 中的“条件b”关于尺度与数量关系的描述反映了在城市系统或网络相关统计中的一项普遍事实，即城市及其要素的排名和大小（如面积、人口、建筑高度等）关系通常遵循齐普夫定律（Zipf’s Law）[44]所描述的幂律分布[45-46]。故凸形的r-s 分布可被用于检测各案例凸形尺度间的内在关系，解释凸形尺度层级结构的存在。其次，分析采用偏度（skewness）和峰度（kurtosis）来检验凸形大小—频率（size-frequency，下称s-f）分布的不对称性，以明确和完善“条件a 和b”中关于尺度、数量、多样性和连续性的描述[47]。以上分析可通过SPSS 软件的统计描述来完成。
3.1 初步统计与定性解读
各研究区域内凸形的数量、面积如表1 所述。其中，罗马、剑桥和佛罗伦萨这三个范型城市案例中的凸形数量（分别为609、1 466、998）皆显著高于后面三个对照城市，且它们最小、最大以及各段百分位数（25%、50%和75%）所对应的凸形面积皆显著低于后三者。其中，各组凸形的数量多寡、面积的最大和最小值的差异程度可支持“条件a”中关于“多样性”的描述。
表1 各研究区域的凸形数量与面积统计
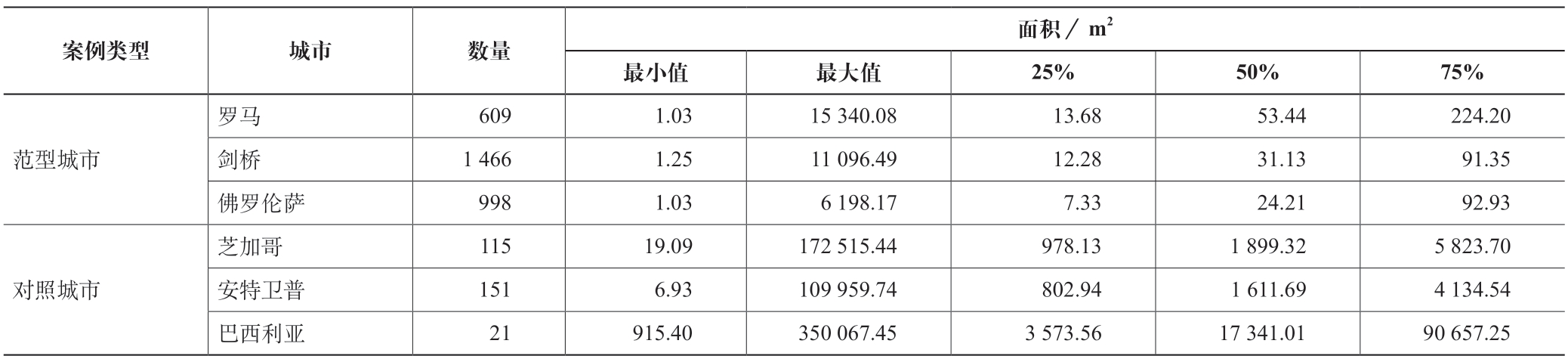
单独考察各区域内面积最大的一组凸形①各组凸形数量间的差异较大，故将各案例中的凸形按面积从大到小进行排名，在排名的对数尺度上选取位于前半段的凸形，以减少该差异。的地理位置可发现，在范型城市中，这些大型凸形的关联性较少，半数以上呈现为联系松散的广场型活动空间；而在对照城市中，最大凸形之间的相互关系密切，往往相互邻接或紧凑排列（图5）。比较它们的形状指数[48]可发现，在范型城市中，该指数的均值相对更接近1，即形状相对更趋近广场型②本文判定广场型空间采用的是形状指数，即凸形周长与相同面积的紧凑图形的周长之比。本文以圆形为紧凑图形，计算公式为P/（2√πA），其中P 代表凸形周长，A 代表凸形面积，当数值越小且接近1，则表明该形状越趋近广场型。，且该趋势随凸形面积增大（排名往前）而越发明显（表2）。综上，范型城市中的最大一组凸形往往就是区域内的主要广场，分散于各处，并处在宜人的尺度范围内，符合“条件c”的描述。相反，对照城市中的最大凸形则多为战略性的轴线，其尺度和形状都无法为社会活动提供必要的聚集感或场所感，不符合“条件c”的描述。
表2 面积最大的一组凸形的形状指数统计
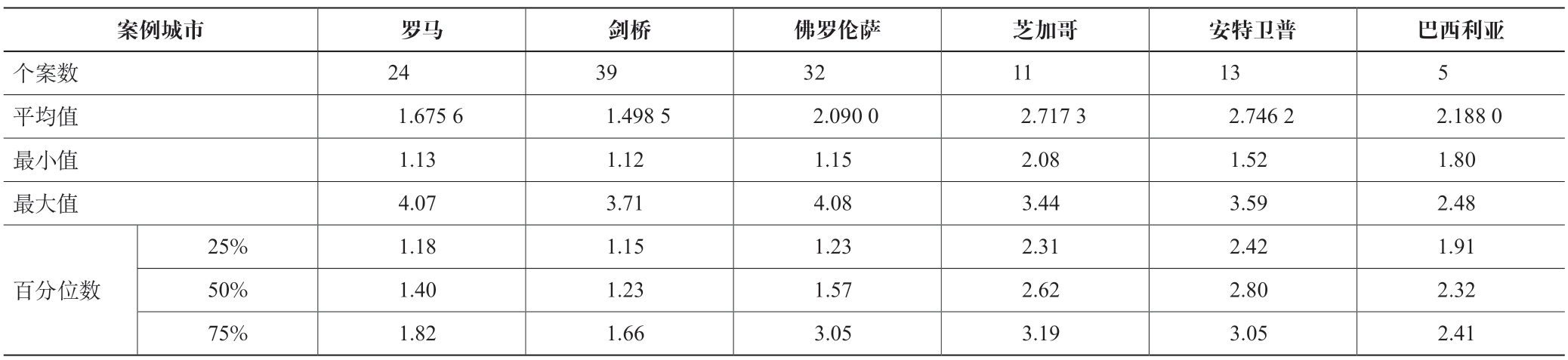
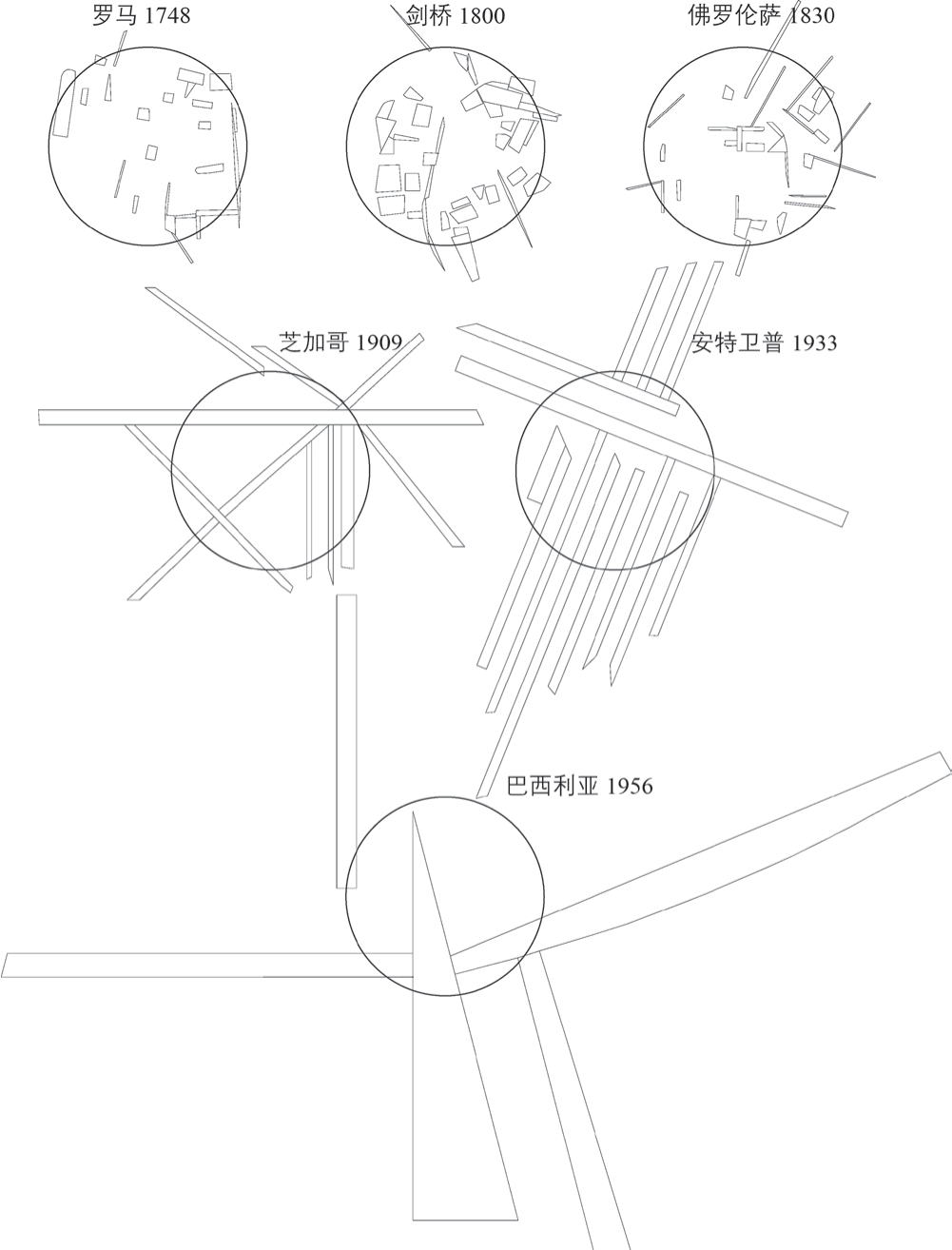
图5 面积最大一组凸形的地理空间关系
3.2 凸形r-s 分布
根据齐普夫定律，将各组凸形按面积大小进行对数排序。据此，r-s 分布如图6 所示，横坐标为凸形从大到小的对数排序，纵坐标为凸形面积的常用对数①排序和面积亦可用自然对数，两者结果等效。。首先，从总体上看，这些数据的拟合直线斜率在-1.5 左右（除巴西利亚外），拟合度（R2）在0.8 以上（除安特卫普），拟合度较为显著，有显著的“长尾”特征，可视为接近齐普夫定律的一种表达②一般而言，斜率接近-1 可视为标准齐普夫定律（pure Zipf’s Law），详见参考文献[44]。。其中，剑桥的数据有着最显著的拟合度（0.92），这或许与之生成最多的凸形数量有关，也可能因为该城市尺度较小，故研究区域覆盖的城市功能相对完整，相关数据更为全面。
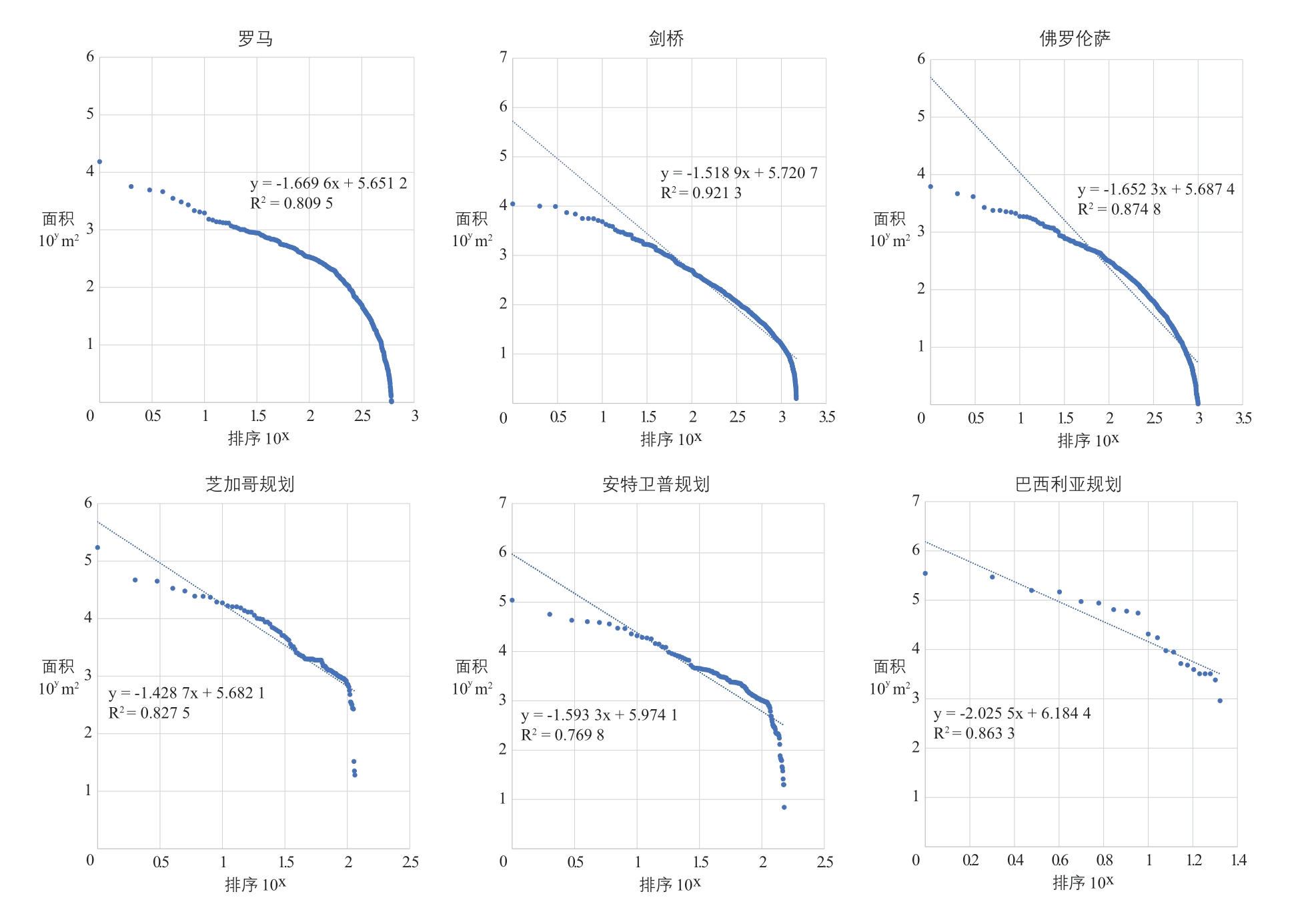
图6 凸形r-s 分布
其次，对照城市组的凸形分布显示，巴西利亚的拟合直线斜率绝对值较大，结合偏少的凸形数量，说明其尺度变化突兀；安特卫普数据分布的拟合度较低，图像显示排名在100 之后的凸形的面积下降变化过快，表明这些凸形尺度的连续性同样不佳。相似情况也出现在芝加哥案例中，尽管它有着较高的拟合度，但分布曲线呈现明显的阶段性变化。鉴于此，笔者进而对比了各组分布的尾部（排名后50%的凸形）（图7），结果表明对照城市和范型城市在此段的分布差异显著。
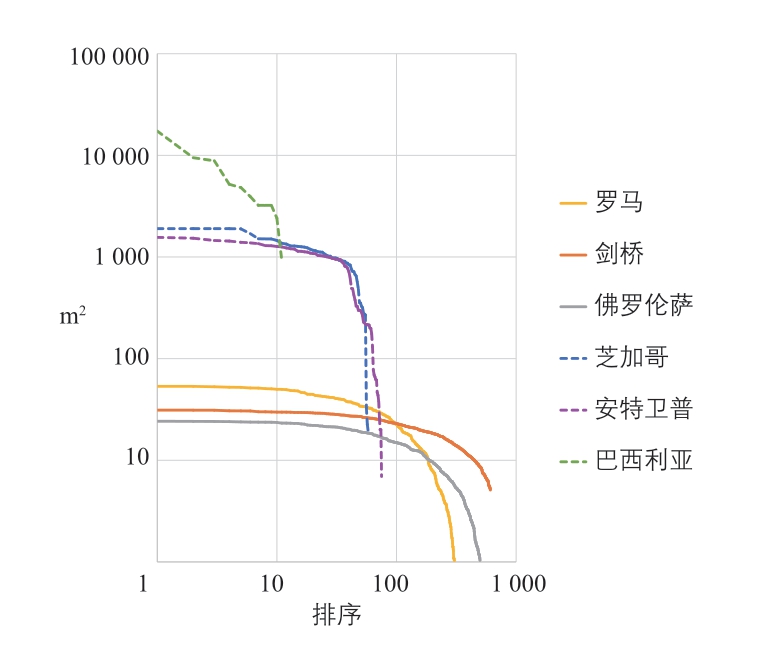
图7 各组凸形r-s 分布尾部对比
综上，“条件a 和b”所描述的趋势能显著地体现在范型城市的凸形r-s 分布上，在对照城市中的表现则不够明显。分析进一步明确了“条件b”中描述的尺度分布应与幂律分布有关，可用r-s 分布形态及其回归直线的斜率来检测；并建议“条件a”中的“连续性”应以“多样性”为前提，可用上述分布的拟合度来衡量。这一定量分析结果表明凸空间及其系统作为检测对象能有效地区分这两类不同的建设逻辑。
3.3 凸形s-f 分布
为了进一步消除“条件b”中关于“极少、较少和极多”描述的模糊性，分析以偏度和峰度作为主要指标检测了凸形的s-f 分布情况。偏度用于检测分布不对称性的方向和程度，其公式为：
其中S 为偏度，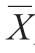
为均值，σ 为标准差。S=0 表明分布对称，即标准正态分布；S >0 分布右偏，即峰尖在左，长尾在右；S<0 则相反。S 的绝对值越大表示不对称程度越高，凸形数量随面积变化的分布趋势越显著。
峰度用于描述分布形态的峰尖陡峭程度，其公式为：
其中K 为偏度，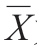
为均值，σ 为标准差。K=0 表明分布为正态峰；K>0 峰尖比正态峰陡峭，其值越大表明陡峭程度越高，即处于该区间的凸形数量越多；K<0 则相反。
凸形s-f 分布形态如图8 所示。其中，凸形频率随面积的变化在范型城市（尤其是剑桥和佛罗伦萨）案例中显得较为连续，而在对照城市中呈现出较大的起伏。各分布形态的偏度和峰度的计算结果如表3 所示。很明显，除巴西利亚外，其他区域的凸形s-f 分布均属于严重偏态分布，峰尖陡峭，长尾在右。该趋势在范型城市的案例中更为显著①若再将标准误作为除数计算在内，两组的差异还将更显著。。可见，偏度和峰度数值能客观反映条件b 中的“极少、极多”等描述，而分布形态的连续变化趋势可用于阐明条件a 中关于可读性的如“协作”和“自然尺度层级”等主观描述。
表3 各研究区域的凸形s-f 分布描述
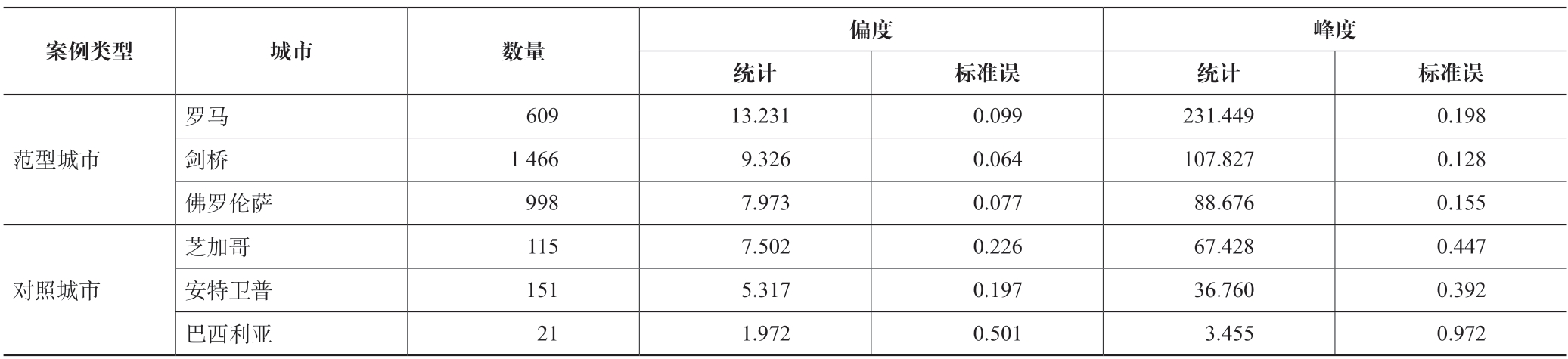
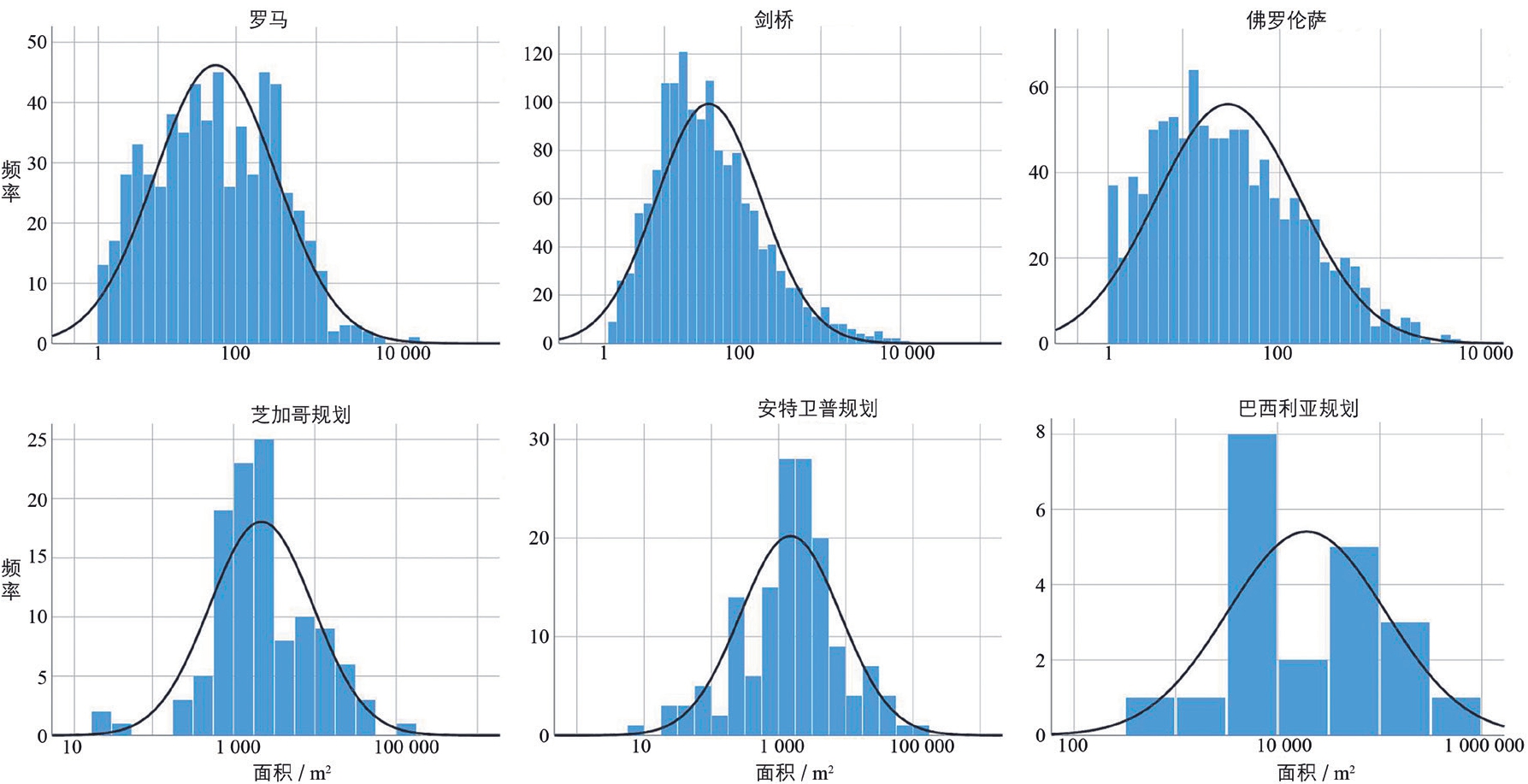
图8 凸形s-f 分布
注：为方便阅读，横坐标为对数尺度。
3.4 分析小结
分析结果汇总如表4 所示。总体上看，各组凸形的r-s分布和s-f 分布具有一定的相似性，其显著程度、偏度和峰度与凸形的数量关系不大，例如：在凸形数量最少的巴西利亚案例中，其r-s 分布具有比罗马案例更高的拟合度；而罗马案例中的凸形并不是最多的，但它们在s-f 分布中呈现的峰尖却是最靠左且最陡峭的。这说明上述数据分布结果大体上符合一般性规律，体现了数据的可靠性和凸形划分方法的合理性，同时也显示出统计结果也许会受图—底平面制图精度的影响，但不足以撼动分布的规律特征。具体来看，范型城市和对照城市空间在各项尺度分布上的异质性主要体现在分布曲线的变化趋势上以及各项定性分析中，并集中表现在r-s 分布的尾部特征、偏度、峰度和最大一组凸形的形状指数的差异。
表4 分析结果汇总
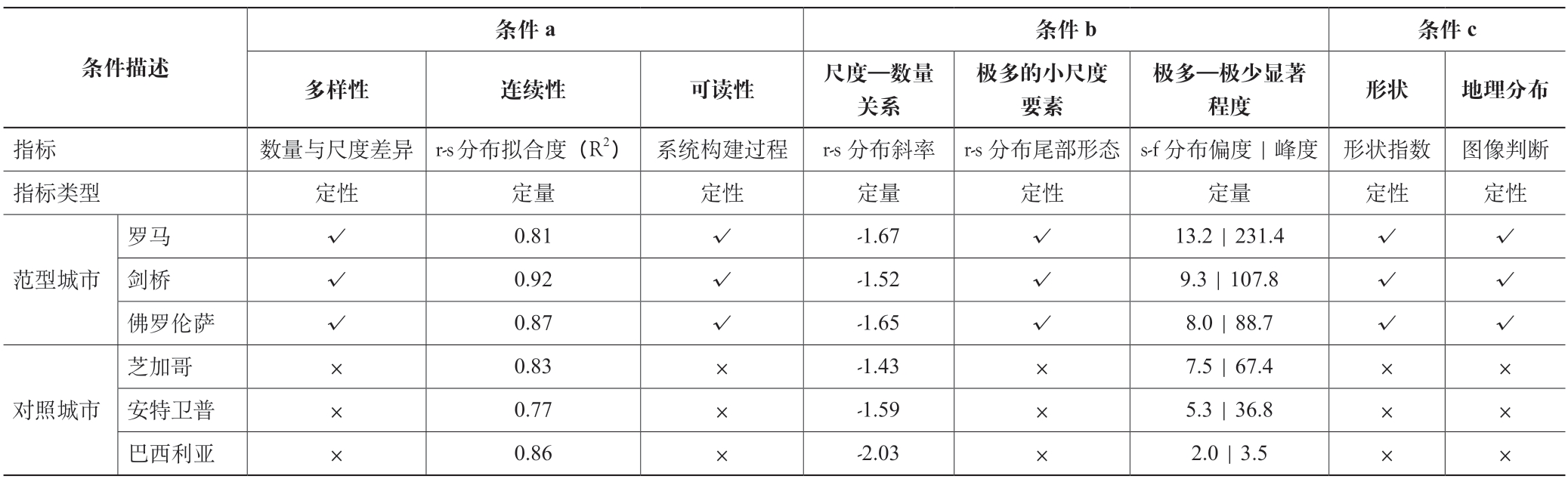
注：√表示数据或判断符合条件描述；×表示数据或判断不符合条件描述。
综上，凸空间的概念、凸空间系统的构建，以及系统中凸形的数量和面积的统计分析，能有效地解析城市建设艺术中的空间尺度法则，减少了描述的多义性和模糊性，并提升了其客观性和准确性。据此，这些原则可更明确地表述如下。
城市的开放空间可基于空间感知原理转化为由凸形组成的凸空间系统，在该系统中：
a′.所有凸形的尺度和按尺度大小的排名关系应遵循幂律分布，其回归直线斜率接近-1，拟合度显著（R2>0.8）；
b′.所有凸形的尺度和频率关系分布应呈严重偏态（长尾偏右的对数正态），具有明显的长尾和尖峰特征；
c′.面积最大的一组凸形应以广场型为主，且应避免地理空间上的密切关联所导致的竞争关系。
4 讨论：尺度美学的形成机制
关于人类建成环境的审美感知通常难以言表，但前面的分析结果为空间美学提供了一类描述和解释：范型城市的开放空间形态看似随机，但隐含着由局部关系构成的一系列具有普遍性的尺度规律；相反，近现代规划所主张的秩序则表现为在平面上机械地重复着少数几种形态类型或结构，忽略了不同尺度之间的协作关系。
4.1 凸空间的竞争与失配
西特及其追随者曾多次提到广场的封闭性、中心空敞、风车形道路开口、沿周边设立纪念物等众多较为琐碎的艺术原则，但他们未能对此类原则作出统一的归纳或解释。通过2.2 小节展示的凸形的生成过程可以发现，上述原则和两个或多个潜在凸形的大小“竞争”有关。例如图3 中的α1 和β1、α2 和β2，因面积相近而构成了竞争关系。在对照城市案例中，此类竞争多出现在大尺度的凸形之间，这往往导致实际的凸空间带给人的真正感受与方案设想之间的失配。
例如在芝加哥规划这类放射形空间结构中，竞争会出现于广场与毗邻的大型街道之间。广场的完整性往往被贯穿而过的大道所消解，如图9 的红色高亮部分所示的广场型空间未能在与轴线型空间I、II、III 的竞争中保持应有的完整性。同理，我国城市新区不少开放空间也因此呈现破碎化。如图10 所示的杭州钱江新城CBD 区域内的轴线广场（图中标有a 的红色高亮部分）因为更大尺度的凸空间I 和II 的影响而失去了感知上的完整性；再如图10 中的剧场广场（b）所对应的凸形因受一侧圆形建筑的影响而未能实现原本设想的形状和围合感。
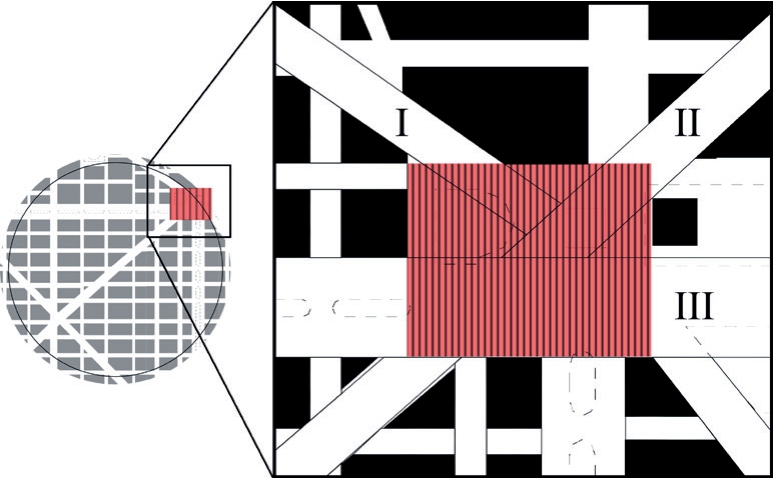
图9 芝加哥规划案例局部凸形关系
资料来源：作者根据自参考文献[38]绘制
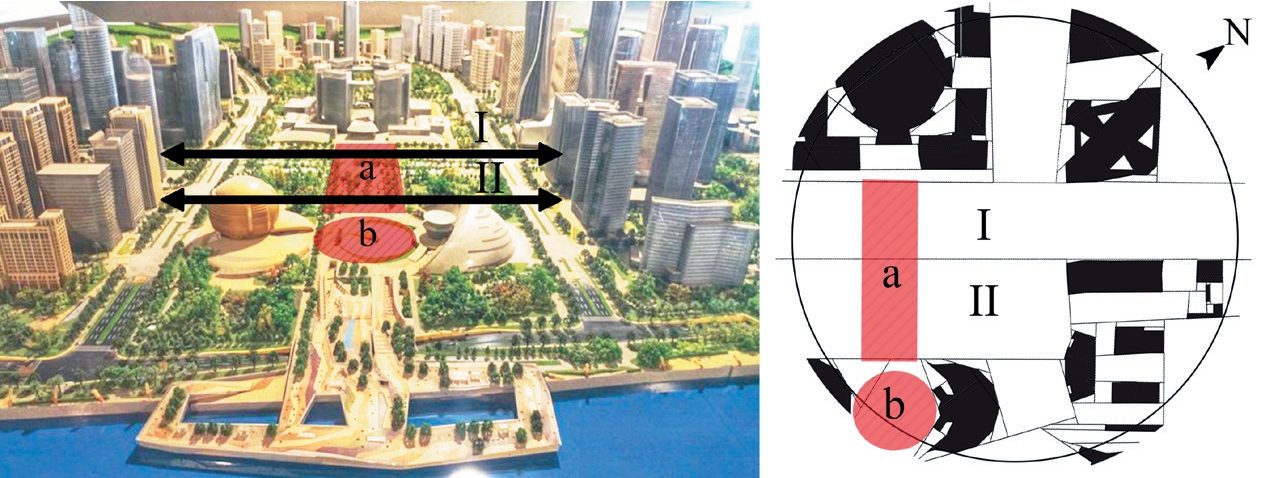
图10 杭州钱江新城CBD 模型局部（左）和该区域内部的凸形关系（右）
资料来源：左：作者摄于杭州钱江博物馆（2021 年）；右：作者基于国家地理信息公共服务平台天地图（https://map.tianditu.gov.cn）绘制
这种由凸空间系统生成规则引发的“竞争”可用于重新理解西特对一个剧院布局的改进实验（图11 左）。在改进前，代表广场的凸形I 潜在的主导地位被代表街道的凸形II 和III所削弱（图11 中）。但通过在剧院T 周边添加柱廊和灯柱（图11 中的a 和b）等微小的改动，减小了凸形II 和III 的尺度，从而使凸形I 成为该系统中的“最大凸形”；同时凸形II 也从街道变为广场（长宽比<3）（图11 右）。这样，原本所设想的广场的封闭感便回到了剧院周围，且空间尺度的变化也更连续了。可见，一系列未被归纳的琐碎的艺术原则可通过上述方法得以统一解释为“避免由空间竞争而导致的可读性降低”，以防止空间形式与感知的失配。至此，通过对凸空间系统构建过程的分析，对近现代规划如何失去建设艺术这一问题提供了一种解释。
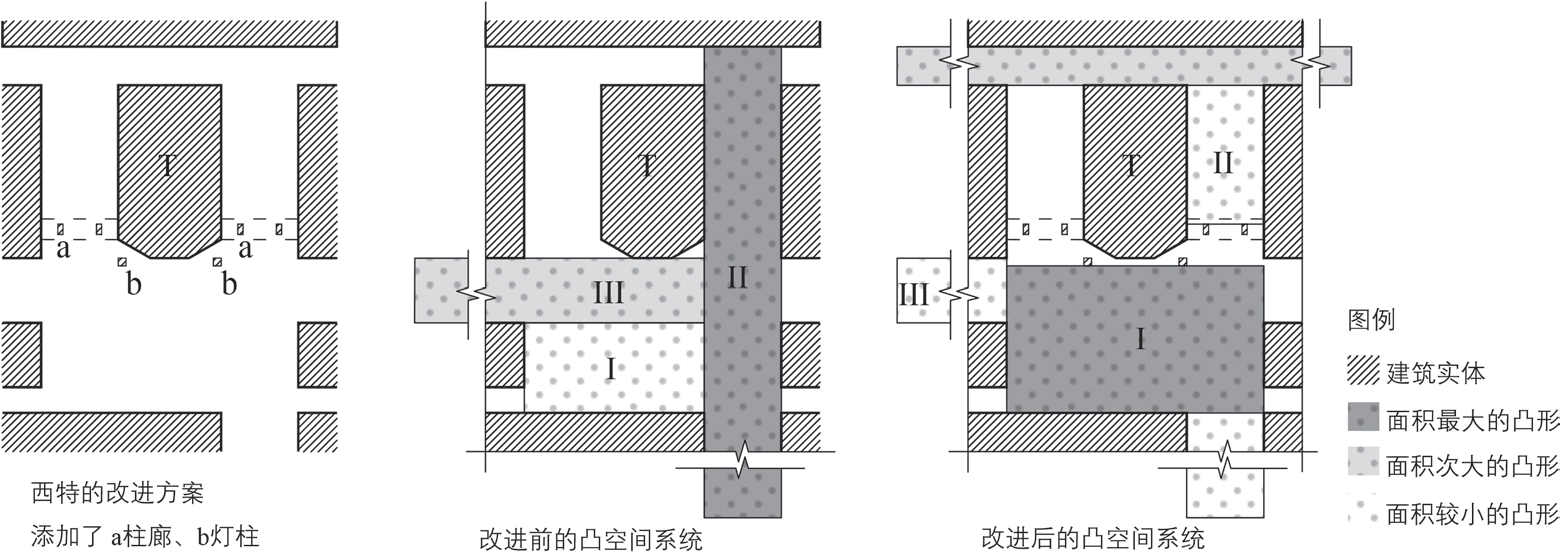
图11 从凸空间系统构建的角度对某剧院改进方案的解释
资料来源：作者根据参考文献[1]图92 绘制，其中内容、布局和部分比例经过了改动
4.2 尺度的组织艺术
空间尺度的艺术原则主要涉及尺度自身的宜人性和尺度之间的协作关系。时至今日该协作关系的缺失仍广泛见于世界各国城市的新区规划中[49-50]。例如：关成贺和罗（Guan &Rowe）检测了北京、上海和深圳的城市中心、边缘和郊区的街区r-s 分布情况，显示三个城市边缘和郊区的街区尺度相较中心具有非连续性递增的趋势[46]。尽管分析对象不同，上述趋势与本研究发现的相似之处在于，经过规划的城市新区往往会更重视大尺度的空间结构，易忽略尺度的多样性和连续性。这也许能归因于实践中尺度组织形式的隐匿性，需要定量分析加以揭示。
尺度的组织艺术未必仅存于前工业时代的城市中，其缺失也不止于某些规划图纸上。对芝加哥（2009 年）和杭州钱江新城片区（2022 年）实际情况的凸形统计分析能支持这一点（图12）。两者凸形的r-s 分布皆有很高的拟合度（分别为0.93 和0.91）。其中，前者的斜率（-1.30）比之前任何一组分布都接近齐普夫定律；而后者相反，其斜率（-2.69）说明该系统的凸形尺度变化剧烈，尤为缺乏连续性。前文的分析也表明这其中存在不少较严重的空间形式与功能的失配现象。作为对比，当代芝加哥相比之前的规划图多了大量小尺度的开放空间，它们多由建筑中庭与界面缺口构成。说明在实际发展中，其凸形r-s 分布“长尾”的缺失部分被有意识地补足了。尽管如此，它的分布曲线的中段仍有明显的阶段性变化，这或许说明此类小尺度空间的完善仍未能充分影响到整体的空间结构。
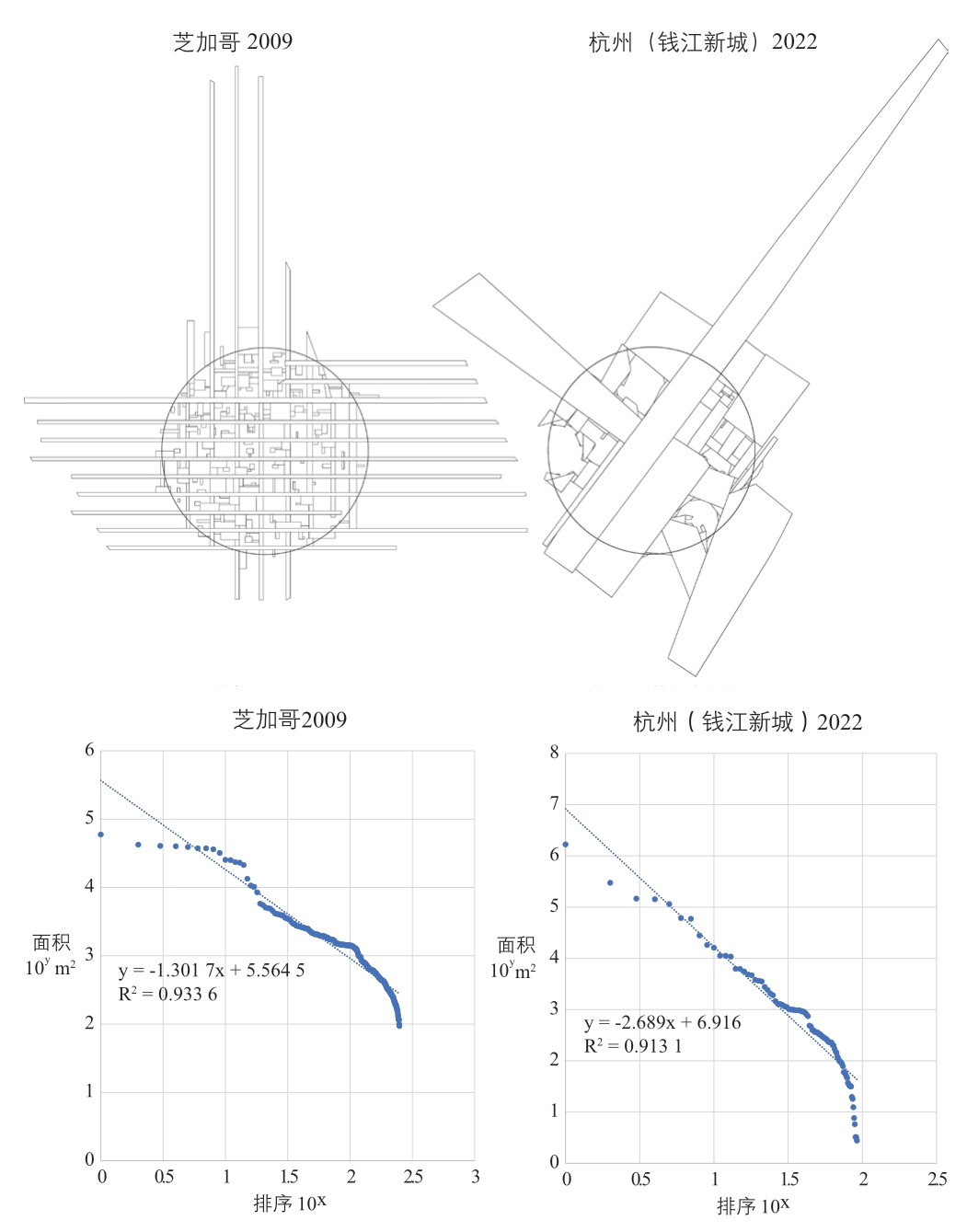
图12 芝加哥和杭州钱江新城研究区域内的凸空间系统与凸形r-s 分布
资料来源：左上为作者基于2009 年芝加哥历史中心图—底地图（https://afterburnham.com/chicagos-historic-center/3-6-03-2009-figure-ground-of-chicagos-greater-historic-center-existing）绘制；右上为作者基于国家地理信息公共服务平台天地图（https://map.tianditu.gov.cn）绘制
最后，回到图3 中有关α3 的问题。诚然，α3 难以反映人们对该空间形状、大小的感知，它代表更多的是某类城市形态中频繁出现的一类统计数据（图13a）。那么，不妨假设没有α3 的情况，这要求A、B、C、D 四个点大致处在同一直线上（图13b）。显然，该假设反映的是近现代规划对“笔直”“秩序”的偏爱。反之，此类统计数据反映的是主要空间之间平缓且自然的衔接，解释了前文r-s 分布和s-f 分布中“长尾”的部分构成，充当着空间转换的过渡和延续。而此类凸形鲜见于新的芝加哥（2009 年）案例，其尺度分布的“长尾”通常由人为营造的小空间来补足，因此它们之间的衔接略显断裂。这或许也说明，范型城市空间之美的特别之处还来自那些此消彼长的凸空间共同作用的宏观结果，而不是刻意安排或处理的细节。
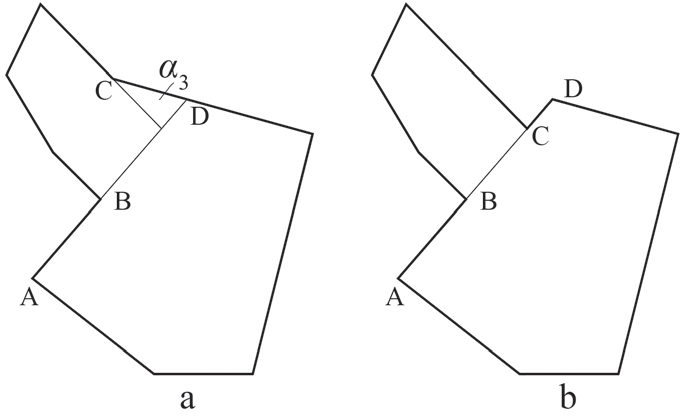
图13 凸形α3 的产生与缺失
4.3 空间作为系统的美学
关于城市空间美学系统化的认识可追溯至凯文·林奇（Kevin Lynch）对城市意象五要素之间关系的解读，而将其系统地纳入量化分析则始于亚历山大（Christopher Alexander）和希利尔等人的贡献。尤其是希利尔创立的空间句法[51]，它不仅将凸空间在城镇聚落分析中的概念和解释系统化，还为较早的迈克尔·本尼迪科特（Michael Benedikt）提出的视域（isovist）理论提供了进一步量化研究的基础。今天诸多空间视觉分析都建立在对这两者的理解之上[52-53]。
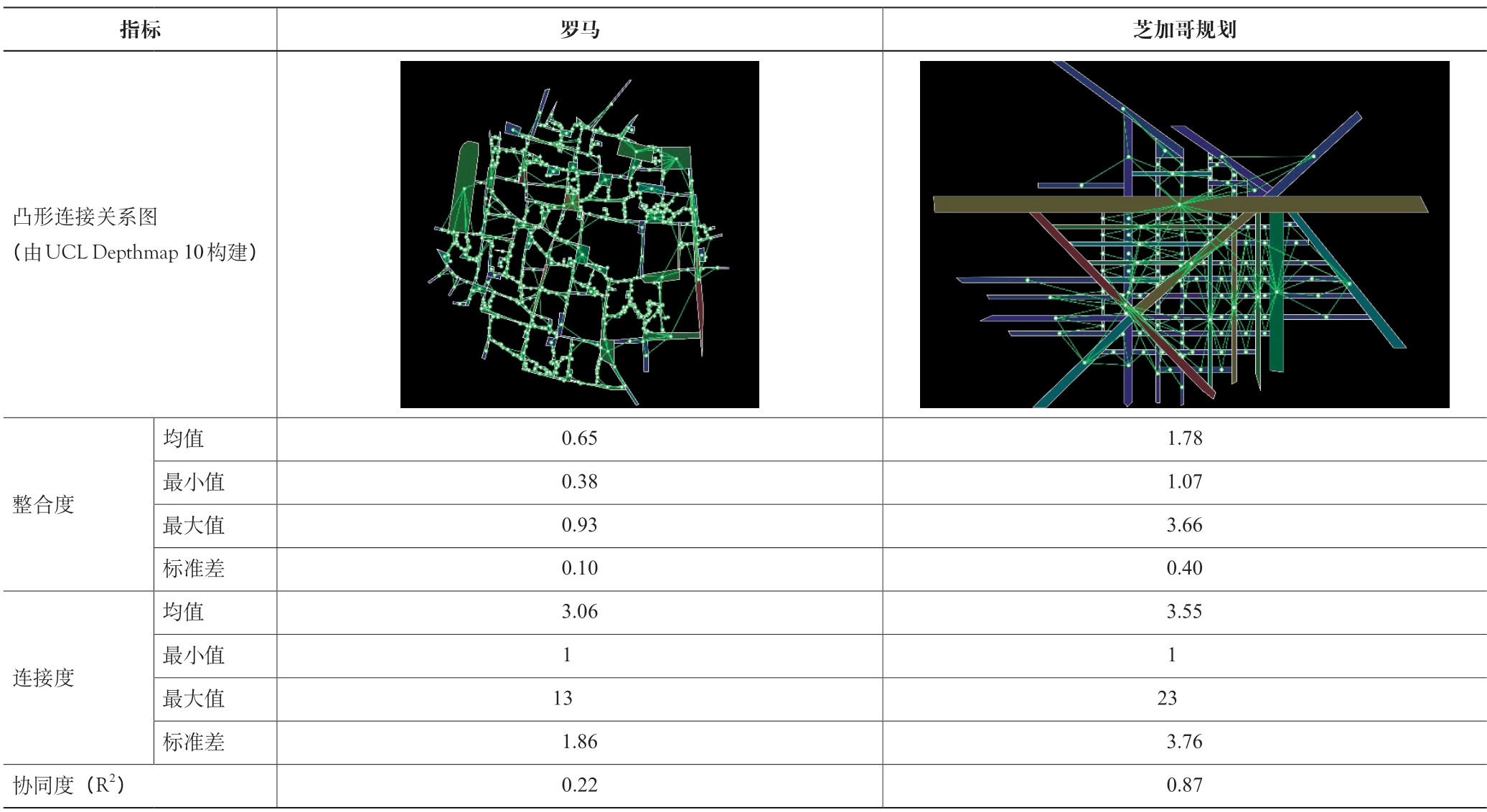
空间的尺度艺术亦可从系统美学的角度来解析。通过罗马和芝加哥规划案例中的两组凸形的空间句法分析可发现，前者凸形的整合度和连接度的各项指标均明显小于后者，且没有显著的协同度①协同度也称可理解度，反映为全局整合度和局部整合度相关性（局部整合度取步数半径为3），体现空间系统的自相似性，见参考文献[51]。（表5）。结合本文主题来说，这意味着罗马案例中凸空间之间的联系较简单，由此构成的序列感甚于冲突感。不管从图像还是数据来看，该系统在表象上更接近希利尔和汉森所归纳的“珠环状”[20]。换言之，该开放空间具备叙事性，有着迷宫般难以预测的变化与走向，被赋予未知的新鲜感，这或许贡献了另一类审美体验。
表5 罗马和芝加哥案例中凸形的空间句法指标对比
5 结论、不足与展望
近年来新兴的城市科学已逐渐建立起基于海量数据的空间研究方法，在复杂而多样的现实环境中揭示了不少与尺度有关的特征规律。本研究亦得益于此，其中最显著的莫过于巴蒂及其团队针对城市诸要素的规模和排序关系的大量研究[54]，它们揭示了事物在变化、竞争中普遍遵循的尺度分布规律，亦从动因的角度揭示了一种难以被自上而下决策所影响的内在规律。
凸空间的概念及其系统的构建皆源自人类的空间美学经验，对它们的分析超越了建设艺术的经验性描述和归纳，为相关尺度法则提供了一种更为客观明确的解析。该解析不仅探讨了欧洲古典城市的开放空间形态何以成为西特眼中的艺术典范的诸多特征，更重要的是，它揭示了西特未曾涉足的层面——基于空间系统的尺度组织艺术。开放空间可视作由一组凸形组成的空间系统，当这些凸形的大小—数量关系呈现为齐普夫定律所描述的状态时，空间的尺度协作就有了实现的基础。在平面地理关系上，良好的协作还要求其中较大尺度的凸形绕开彼此的竞争，并鼓励较小尺度的凸形充当它们之间的衔接和过渡。显然，此类艺术特征并不显现于任何静态画面上，而是隐匿在整体的动态体验中，也正因为近现代规划忽略了这些尺度在整体上的协作，导致它们在无意中割裂了城市。
虽然艺术原则未必是解决当代城市症结的唯一处方，但作为人类文化遗产的独特价值，今天对它们的解读仍有必要，从中归纳而来的尺度规律也值得继续探讨。尤其是开放空间尺度结构的完整性、多样性和连续性，对我国现阶段的城市更新实践有重要借鉴意义。对照城市案例的解析表明，仅凭全局的秩序构建难以实现尺度的层级协作，因为全局秩序无法足够具体地落实到小尺度层级上。而仅靠建筑表面的变化也不能撼动整体尺度相对稳定的分布规律，正如西特的剧院改进案例也恰恰表明，弥补物质形态规划的缺失往往需要突破建筑红线范围的约束。简言之，建筑设计与空间规划之间缺少一个（或一些）中介层级。那么，在尺度上更为灵活的城市设计或景观设计也许能胜任这项衔接工作，本研究提出的凸空间系统则为之提供了一种定量检测和评估的手段。
另外，分析所选的案例虽具有代表性，但数量毕竟太少，在面对现实城市的繁复多样时难免显得捉襟见肘。一方面，我们有希望通过完善分析算法来扩大研究的案例范围，另一方面，人工分析也能提供更丰富的见解和启示，因此两者并用或许是拓展研究更有效的办法。
注：文中未注明资料来源的图表均为作者绘制。
审稿专家的建议为提升本文质量提供了很大的帮助，特此致谢。
[1] 卡米诺·西特.城市建设艺术: 遵循艺术原则进行城市建设[M].仲德崑,译.南京: 东南大学出版社,1990.
[2] GIBBERD F.Town design[M].3rd ed.London: The Architectural Press,1959.
[3] MOUGHTIN C.Urban design: street and square[M].Burlington,MA:Architectural Press,2003.
[4] KRIER R,MICHAEL G,HANS I,et al.Town spaces: contemporary interpretations in traditional urbanism[M].2nd ed.Basel: Birkhauser,2006.
[5] MARSHALL S.Cities,design &evolution[M].London: Spon Press,2008.
[6] 孙施文.后现代城市规划[J].规划师,2002,6(18): 20-25.
[7] 吴其煊,刘济瑀,闫文凯,等.天津八大里项目数字城市UIM 理念讨论[C]// 第十七届全国工程建设计算机应用大会论文集.人民交通出版社,2014: 241-247.
[8] HU M,CHEN R.A framework for understanding sense of place in an urban design context[J].Urban science,2018,2,34.DOI: 10.3390/urbansci2020034.
[9] LAWSON B.Language of space[M].Oxford: Architectural Press,2001.
[10] TRANCIK R.Finding lost space: theories of urban design[M].New York:John Wiley &Sons,Inc.,1986.
[11] 菲利普·巴内翰,让·卡斯泰，让-夏尔·德保勒.城市街区的解体[M].魏羽力,译.北京: 中国建筑工业出版社,2012: 9.
[12] MARSHALL S.Streets and patterns[M].London: Spon Press,2005: 9.
[13] 韩西利,彼得·斯约斯特洛姆.城市感知: 城市场所中隐藏的维度[M].北京: 中国建筑工业出版社,2015.
[14] 彭坤焘,张雪.规划话语中空间尺度悬置现象的剖析与反思[J].国际城市规划,2021,36(4): 10-16.DOI: 10.19830/j.upi.2021.147.
[15] 尼科斯·萨林加罗斯.城市结构原理[M].阳建强,程佳佳,刘凌，等译.北京: 中国建筑工业出版社,2011.
[16] GEHL J.Cities for people[M].Washington,DC: Island Press,2010.
[17] SALAT S.关于可持续城市化的研究：城市与形态[M].陆阳,张艳,译.北京: 中国建筑工业出版社,2012.
[18] THWAITES K,SIMKINS I.Experiential landscape: an approach to people,place,and space[M].London,New York: Routledge,2007.
[19] 尼科斯·萨林加罗斯.建筑论语[M].吴秀洁,译.北京: 中国建筑工业出版社,2010: 58.
[20] HILLIER B,HANSON J.The social logic of space[M].Cambridge:Cambridge University Press,1984.
[21] 芦原义信.街道的美学[M].天津: 百花文艺出版社,2006.
[22] ALEXANDER C,ISHIKAWA S,SILVERSTEIN M.A pattern language:towns,buildings,construction[M].Oxford: Oxford University Press,1977.
[23] RASMUSSEN S E.Experiencing Architecture[M].New York: John Wiley &Sons,Inc.,1959.
[24] HEBBERT M.Figure-ground: history and practice of a planning technique[J].Town planning review,2016,87: 705-728.
[25] SALINGAROS N.Life and complexity in architecture: from a thermodynamic analogy[J].Physics essays,1997(10): 165-173.
[26] CAMONA M,TIESDELL S,HEATH T,et al.Public places urban spaces:the dimensions of urban design[M].2nd ed.Oxford: Architectural Press,2010.
[27] LYNCH K.The image of the city[M].Cambridge,MA: MIT Press,1960.
[28] 阿尔多·罗西.城市建筑学[M].黄士钧,译.北京: 建筑工业出版社,2006.
[29] 格哈德·库德斯.城市结构与城市造型设计[M].秦洛峰,蔡永洁,魏薇,译.北京: 中国建筑工业出版社,2006.
[30] 克里斯蒂安·诺伯格-舒尔茨.居住的概念——走向图形建筑[M].黄士钧,译.北京: 中国建筑工业出版社,2012.
[31] 朱蓉,吴尧.城市·记忆·形态：心理学与社会学视维中的历史文化保护与发展[M].南京: 东南大学出版社,2013.
[32] 郭龙.记忆与想象：城市认知的双重维度[J].建筑学报,2016(12): 94-97.
[33] PEPONIS J,WINEMAN J,RASHID M,et al.On the description of shape and spatial configuration inside buildings: convex partitions and their local properties [J].Environment and planning b: urban analytics and city science,1997,24(5): 761-781.
[34] OSMOND P.The convex space as the ‘atom’ of urban analysis[J].The journal of space syntax,2011,2(1): 97-114.
[35] BEIRÃO J,CHASZAR A,ČAVIĆ L.Analysis and classification of public spaces using Convex and Solid-Void Models[M]// RASSIA S TH,PARDALOS P M,eds.Future city architecture for optimal living (Springer optimization and its applications 102).Springer,2015: 241-269.
[36] OTTO F.Occupying and connecting: thoughts on territories and spheres of influence with particular reference to human settlement[M].Fellbach:Edition Axel Menges,2009.
[37] STAMPS A.Psychology and the aesthetics of the built environment[M].New York: Plenum,2000.
[38] MOODY W D.Wacker’s manual of the Plan of Chicago[M/OL].Chicago:H.C.Sherman,1912: 96.[2022-09-27].http://www.encyclopedia.chicagohistory.org/pages/10418.html.
[39] 勒·柯布西耶.光辉城市[M].金秋野,王又佳,译.北京: 中国建筑工业出版社,2011: 276.
[40] COSTA L.Report of the Pilot Plan for Brasília[R].Brasilia: GDF,1991.
[41] JENCKS C.The language of post-modern architecture[M].6th edn.London:Academy Editions,1991.
[42] KOSTOF S.The city shaped: urban patterns and meanings through history[M].London: Thames &Hudson Ltd.,1991.
[43] KROPF K.Aspects of urban form[J].Urban morphology,2009,13(2): 105-120.
[44] GABAIX X.Zipf’s Law for cities: an explanation[J].The quarterly journal of economics,1999,August: 739-767.
[45] BATTY M.Competition in the built environment: scaling laws for cities,neighbourhoods and buildings[J].Nexus network journal,2015(17): 831-850.
[46] GUAN C,ROWE P.Beyond big versus small: assessing spatial variation of urban neighborhood block structures in high-density cities[J].Socioecological practice research,2021(3): 37-53.
[47] 王学民.应用概率统计[M].上海: 上海财经大学出版社,2005.
[48] 毛亮,李满春,刘永学,等.一种基于面积紧凑度的二维空间形状指数及其应用[J].地理与地理信息科学,2005,21(5): 11-14.
[49] 杨俊宴,吴浩,金探花.中国新区规划的空间形态与尺度肌理研究[J].国际城市规划,2017,32(2): 34-42.DOI: 10.22217/upi.2017.001.
[50] 鲁晓军,门坤玲,翁一峰.新城区建设的空间尺度问题与改进策略刍议[J].城市规划,2015,39(4): 53-57,70.
[51] HILLIER B.Space is the machine: a configurational theory of architecture[M].e-edition.London: Space Syntax,2007.
[52] KOCH D.On aesthetics and spatial configuration[C]// Space Syntax 11th International Symposium,2017,162: 1-14.
[53] ISAACS R.The urban picturesque: an aesthetic experience of urban pedestrian places[J].Journal of urban design,2000,5(2): 145-180
[54] BATTY M,CARVALHO R,HUDSON-SMITH A,et al.Scaling and allometry in the building geometries of Great London[J].European physical journal b,2008,63(3): 303-314.