引言
1980 年以来,土地利用/覆被变化(LUCC: Land Use/Cover Change)成为全球关注的热点问题[1-2]。如今,城市化的进程加快了城市的路网扩张和土地利用变化[3],城市发展和人口增长使得用地空间格局处于动态的变迁和发展中,城市空间的重构与调整等面临着巨大的挑战[4]。城市发展是一个复杂系统的演化过程,城市用地结构的变化是城市发展的重要表现[5]。城市快速发展促进了城市交通发展和路网格局变化,而城市交通是影响城市土地利用格局和未来情景的重要因素[6]。因此,量化研究城市交通模式,探究城市发展与交通的关系对于城市规划和城市的高质量、可持续发展有着重要意义。
在现有的城市发展模拟模型中,元胞自动机(CA:Cellular Automata)模型受到广泛关注[7-8],被大量应用于模拟城市土地利用类型之间的转变[9-10]。传统元胞自动机通常以相同形状规则的像元或斑块作为元胞单元[11],可以模拟城市发展的时空动态变化过程,但在表达土地利用地块的实际形状和精细尺度模拟方面仍存在局限性[12]。现实中的地理实体往往是不规则的多边形。为克服传统CA 模型不能准确反映现实的不足[13],矢量元胞自动机(VCA: Vectorbased Cellular Automata)模型被陆续提出并应用于城市发展模拟[14-15]。VCA 模型一般以德洛内(Delaunay)三角网[16]、街道地块[17]、地籍地块[18]等作为元胞单元模拟土地利用变化。其中,地籍地块能更真实地代表地物几何形状,以此作为元胞单元更接近于真实的城市规划模拟[12,19]。
城市交通作为城市发展的骨架,影响着城市的发展规模和土地利用格局[20]。目前一些学者探究了城市间的相互作用对城市群扩张和大都市区发展的影响[21-22],研究表明空间交互作用在城市景观演化中发挥着重要作用,城市发展模拟需要考虑空间交互的影响。空间交互作用存在着距离衰减的空间效应[23],因此在研究城市土地利用类型的转变时,城市内部不同区域间交互作用所产生的连通性更加值得重视。此外,交通可达性是衡量土地利用与交通系统效率的关键指标,对城市用地的规模、开发强度和空间分布具有指向性作用[24],在城市发展模型中加入可达性因子有助于提高模拟精度[25-26]。
然而,在城市发展模拟研究中,大多数学者较少考虑城市交通的驱动影响,一般将与各等级静态路网的距离作为交通可达性因子,未能挖掘动态交通对城市土地利用变化的影响,以致不能有效表达静态路网和动态交通的综合影响效应。因此,本研究提出了一套基于矢量元胞自动机与交通因素的城市土地利用变化模拟框架(T-VCA: Traffic-based Vector Cellular Automata),该框架将城市连通性因子和交通可达性因子作为模型变量引入矢量元胞自动机模型,有效表达交通因素对城市土地利用变化的影响;同时以深圳市为研究区,在真实地块尺度上分析城市连通性因子和交通可达性因子对模拟城市土地利用变化的影响。
1 研究方法
本研究将量化城市内部不同区域间的连通性和地块交通可达性,并引入元胞转换规则,构建兼顾长距离空间交互影响和短距离可达性效应的城市发展模拟模型T-VCA(图1)。研究主要分为三部分:首先,基于出租车轨迹、地名共现、GDP 和人口数据将城市不同区域之间的空间交互作用量化为城市连通性因子,基于路网数据量化交通可达性因子,并将这两个因子作为交通效应因子引入元胞转换规则;其次,采用随机森林模型计算地块总体发展概率,同时引入邻域效应、限制因子和随机因子,从而计算出每个地块的发展概率;最后,基于轮盘赌策略模拟目标年份的土地利用格局,进行模拟精度评价和景观指数相似度分析。
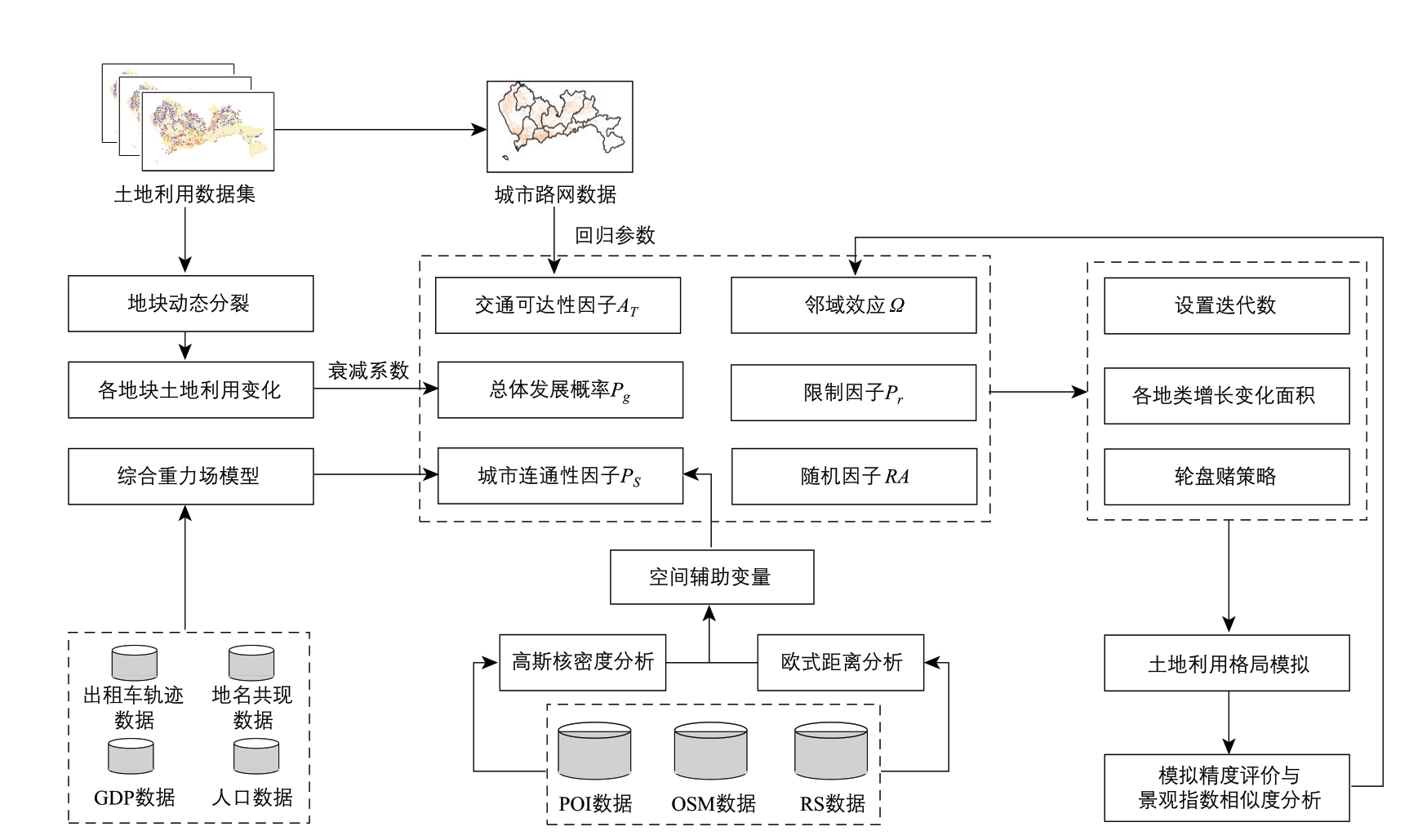
图1 考虑交通因素的城市土地利用变化模拟框架
1.1 挖掘城市交通因素
1.1.1 城市连通性因子度量
城市内的空间交互作用由不同区域之间各要素的流动来实现,其空间交互强度可用重力场模型来量化[27]。由于大城市交通网络和信息网络较为发达,规模不同、经济地位不同的区域之间存在着明显的相互作用,综合交通流、信息流和经济流等数据能够更加准确地感知和度量城市内的空间交互作用对土地利用变化的影响。在距离衰减效应影响下,城市内空间交互作用对元胞的影响可表示为城市连通性因子Psi,公式如下[28]:

式中:城市连通性因子Psi 表示城市不同区域之间空间交互对地块元胞i 的状态转换概率的最大作用值;Fk 为城市k 区域的节点强度;D 为元胞i 的中心到k 区域中心的欧氏距离;β 为距离衰减指数。
距离衰减指数是对空间交互强度在地理距离上衰减速度的度量,许多学者忽视研究的时空背景差异和地理实体的异质性而使用相同的距离衰减指数[29-30]。本研究将重力场模型等式进行对数变换后,将基于出租车轨迹数据的不同区域间的空间交互强度和距离代入得到散点图,通过线性拟合计算斜率作为距离衰减指数[31],从而得到适用本研究的距离衰减指数β。
主成分分析(PCA: Principal Component Analysis)是一种探索性的统计方法[32],该方法的数据挖掘功能可选择变量中的“主成分”用于评估城市实力水平[33]。本研究基于各区域的出租车轨迹、地名共现、人口和GDP 等数据,对区域不同类型的空间交互作用采用PCA 算法量化各区域的节点强度Fk① 空间交互作用的具体量化方式请以手机扫描本文末页的二维码,在公众号“开放科学计划OSID”中查看“本文开放的科学数据与内容”栏目。。
1.1.2 交通可达性因子度量
考虑到元胞自动机的建模受到沃尔多(Waldo)提出的地理学第一定律影响[34],以及模型固有的空间特性,本研究引入交通可达性对土地利用变化的影响[35]。当前许多研究将可达性简单定义为从元胞到最近的公路或铁路等基础设施的线性距离[36-37]。相较于线性距离,努诺等(Nuno et al.)提出的指数可达性模型能更好地量化道路对城市用地的作用[35]。本研究以每个地块为单元,通过获取与当前地块最近道路的距离,根据指数可达性模型计算相应地块的交通可达性因子AT,公式如下:
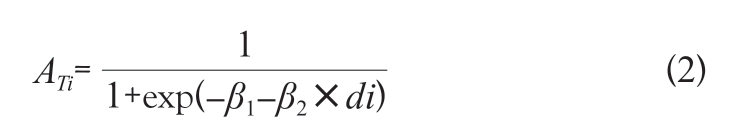
式中:ATi 是地块i 范围内的交通可达性强度大小;β1 和β2 表示回归系数,通过误差校正获取;di 表示地块i 至道路的最近欧式距离。
1.2 构建考虑交通因素的矢量元胞自动机模型
本研究对矢量元胞自动机模型改进的核心是在地块i 范围内引入城市连通性因子PSi 和交通可达性因子ATi,有效挖掘交通因素对城市发展的驱动作用。T-VCA 模型构建方法如下② 具体的构建方法请详见“开放科学计划OSID”,查看方法同注释①。:
式中:![]() 为地块i 在t 时刻发展为第k 类土地利用类型的转换概率,
为地块i 在t 时刻发展为第k 类土地利用类型的转换概率,![]() 为地块i 在t 时刻发展为第k 类土地利用类型的总体发展概率;PSi 是城市不同区域之间连通性对地块i的影响值;ATi 为地块i 在t 时刻的交通可达性强度大小;
为地块i 在t 时刻发展为第k 类土地利用类型的总体发展概率;PSi 是城市不同区域之间连通性对地块i的影响值;ATi 为地块i 在t 时刻的交通可达性强度大小;![]() 为第k 类土地利用类型在t 时刻对地块i 的邻域效应;
为第k 类土地利用类型在t 时刻对地块i 的邻域效应;![]() 为地块i 发展为第k 类土地利用类型的限制因子;RA 为随机因子。
为地块i 发展为第k 类土地利用类型的限制因子;RA 为随机因子。
为了验证所提出的T-VCA 模型的优越性,本研究设定了另外三种模型,分别是基于随机森林的矢量元胞自动机(RFVCA: Random Forest Based Vector Cellular Automata)模型、仅考虑城市连通性的矢量元胞自动机(C-VCA: Connectivity Based Vector Cellular Automata)模型和仅考虑交通可达性的矢量元胞自动机(A-VCA: Accessibility Based Vector Cellular Automata)模型。利用同一套数据进行土地利用变化的模拟,可对比分析不同模型在城市土地利用模拟中的性能。
1.3 模拟精度评价和景观指数相似度分析
为了定量评估土地利用变化的模拟结果以验证T-VCA 模型的有效性,本研究采用优值因子(FoM: Figure-of-Merit)、生产者准确度(PA: Producer’s Accuracy)和用户准确度(UA:User’s Accuracy)对结果进行精度评价。其中PA 表示观察到的变化召回率,UA 表示模拟的变化精度,而FoM 同时结合了PA 和UA 的特点[38-39]。大量研究指出,在大规模模拟中,FoM 达到0.2 以上表示模型具有极强的可用性[18,40-41]。各精度评价指标的计算公式如下:
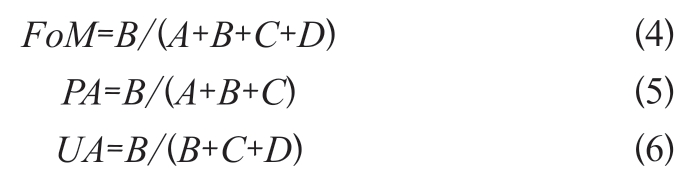
其中,A 表示实际发生用地类型转变而模拟结果保持不变造成的地块面积误差;B 表示实际发生了转变并且模拟结果与实际相同的地块面积;C 表示实际发生转变并且模拟也发生了转变,但模拟发生转变的类型与实际不符造成的地块面积误差;D 表示实际没有转变但模拟发生转变产生的地块面积误差。
景观指数适用于描述和量化景观结构和生态格局,景观指数相似度可以有效度量模拟数据与真实数据之间土地利用模式的一致性[42]。本研究共选取了斑块数(NP: Number of Patches)、最大斑块指数(LPI: Largest-patch Index)、平均欧氏最近邻距离(ENN: Mean Euclidean Nearest Neighbor Distance)和平均周长面积比(PARA: the Mean Perimeter-area Ratio)四种景观指数,并用模拟结果与真实情景的各景观指数之间的平均差异值来衡量景观指数相似度αl,计算公式如下:
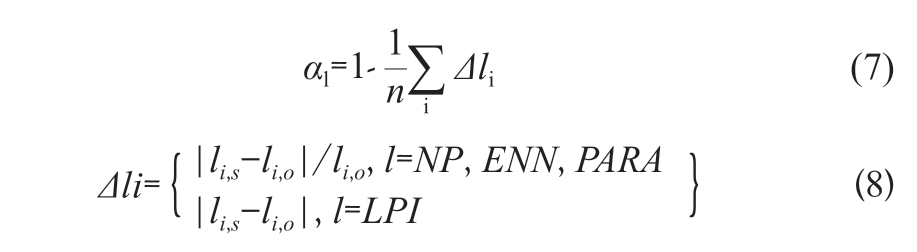
式中:li,s 和li,o 分别表示模拟场景和真实场景的第i 个景观指数;Δli 表示第i 个景观指数的归一化差;αl 表示实际与模拟土地利用之间的景观指数相似度;n 表示景观指数的种类数量① 有关FoM 与景观指数等指标的具体描述详见“开放科学计划OSID”,查看方法同P19 注释①。。
2 以深圳为案例的研究
2.1 案例研究区和数据选取
本文以深圳市为研究区。深圳市作为中国华南地区最发达的城市之一,总面积1 997.47 km2,2021 年常住人口为1 768.16 万人,GDP 达到30 664.85 亿元。深圳市下辖10 个行政区,土地利用模式较为复杂,土地利用类型仍在快速变化中[43-44]。
土地利用地块数据是本研究所用到的重要数据集,来源于深圳市规划和自然资源局官网② 详见https://pnr.sz.gov.cn/。提供的2009—2014 年的地籍土地利用数据。本研究将土地利用地块数据按照五种土地利用类型划分,包括公共管理服务用地、居住用地、商业用地、工业用地和未建设用地。根据官方统计数据,2009—2014 年间,深圳市土地利用地块总数从104 608 块增加到123 325 块,增长率达17.89%(图2)。
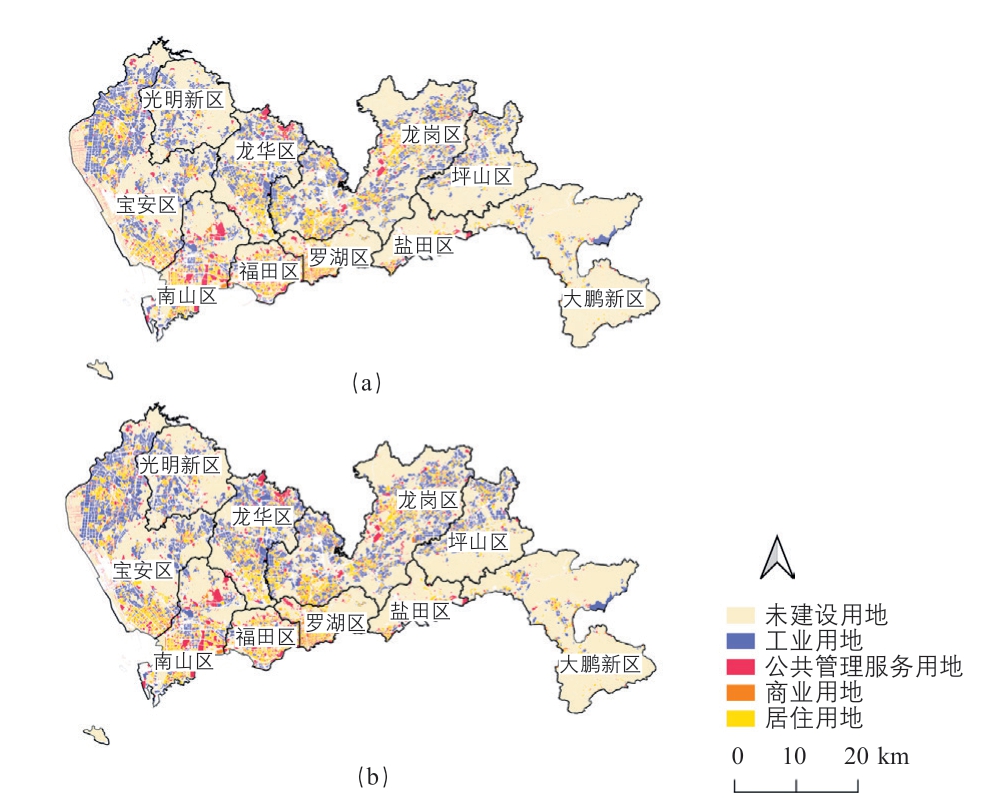
图2 深圳市土地利用类型变化(上图为2009 年;下图为2014 年)
本研究考虑的城市土地利用的驱动因素主要包括地形、交通、工业、商业和居民设施等[45],数据来源于2018 年的高德POI(Point of Interest)数据、OSM(OpenStreetMap)数据以及RS(Remote Sensing)数据。基于这些数据共构建空间辅助变量数据14 类,将其生成欧式距离或基于积分均方误差(MISE: Mean Integrated Square Error)准则的高斯核密度数据[46-47],分辨率设置为30 m,所有辅助变量数据归一化为0~1(图3)。
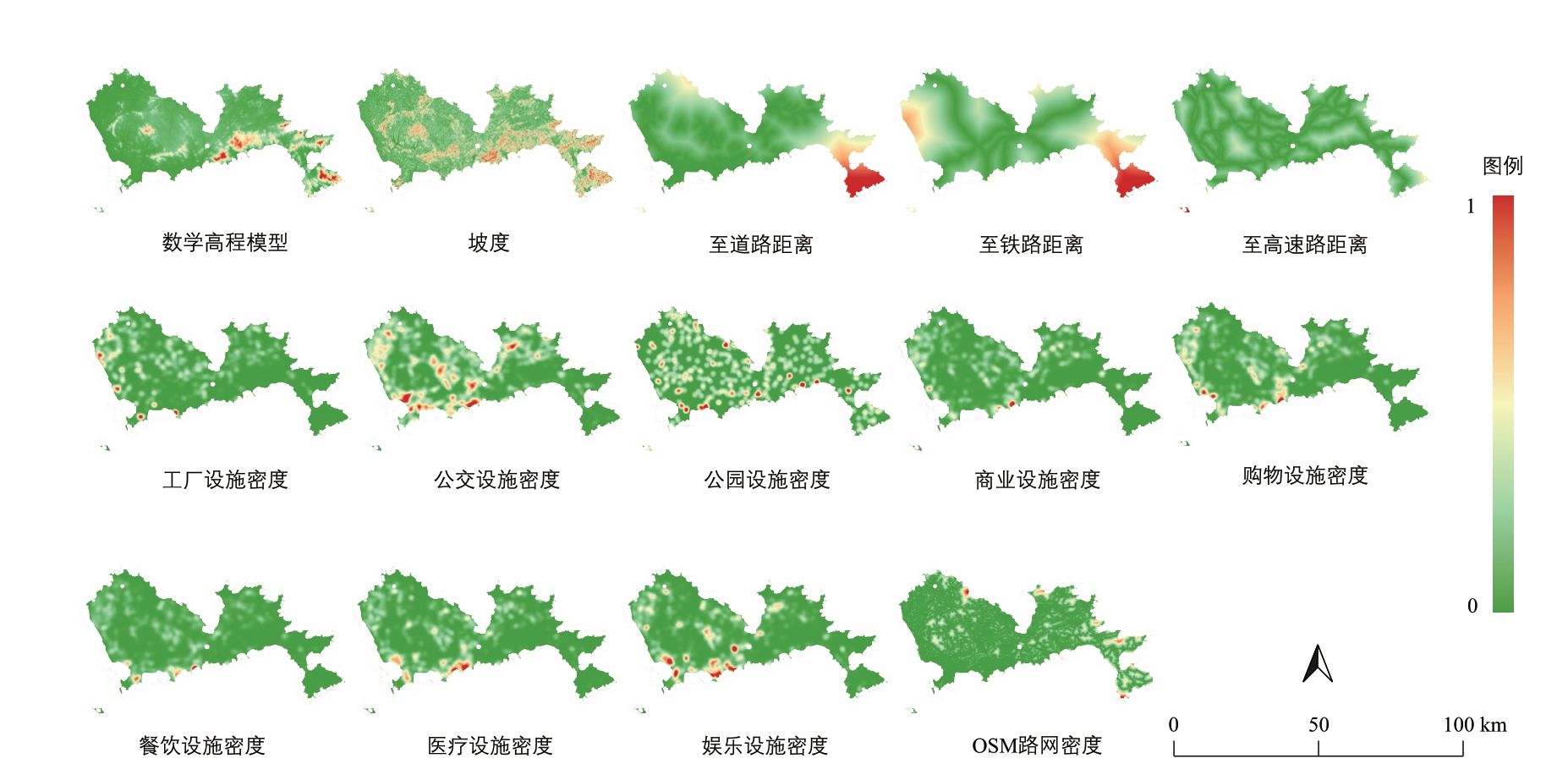
图3 空间辅助变量数据集
本研究从交通流、信息流和经济流的角度选取了出租车轨迹、地名共现以及人口和GDP 数据,对城市内部不同区域之间的交互作用进行模拟。出租车轨迹数据已被广泛用于旅行行为、人员流动性和城市结构等方面的研究,可有效揭示交通出行模式的时空特征[48]。本研究的出租车轨迹数据来源于某大型网约车平台,选取2016 年6 月5—29日,共8 362 辆出租车产生的179 411 113 条记录,每条记录包含车辆的唯一ID 号、GPS 信号时间、经纬度等。地名共现是指互联网网页中同时出现于同一文档的不同地名,两个地名在网页中同时出现,即可体现地名空间之间的联系[49]。地名共现数据具有明确的网络空间结构,能够反映节点的特征[49]。本研究通过新浪新闻搜索引擎获取深圳市不同区域的地名共现数据,将其作为信息流来测度深圳市不同区域之间的交互作用。另外,本研究选取人口和GDP 数据感知经济流的交互作用,数据来源于深圳市统计局① 详见http://tjj.sz.gov.cn/。。
2.2 参数设置与敏感性分析
本研究采用解析法计算距离衰减指数,可确定距离衰减指数β 为1.062(图4)。考虑到交通可达性模型中涉及的两个回归系数β1 和β2 对实验结果的影响,本研究在0~1.4 范围内分别进行了实验,得出交通可达性模型中回归系数的敏感性分析结果图(图5)。可以发现,当回归系数β1=0.2 且β2=0.2 时,T-VCA 模型的模拟精度FoM 达到最高。值得注意的是,回归系数β2 对模拟精度的单独作用比β1 的更大,说明β2 具有更好的灵敏度。当β1 和β2 两个参数共同作用且二者取值在0.2 或0.6~1.0 时,模型的模拟精度效果明显高于单一参数对精度的影响。这也说明城市交通是一个复杂系统,选取合理的参数才能更好地模拟城市真实的发展过程。
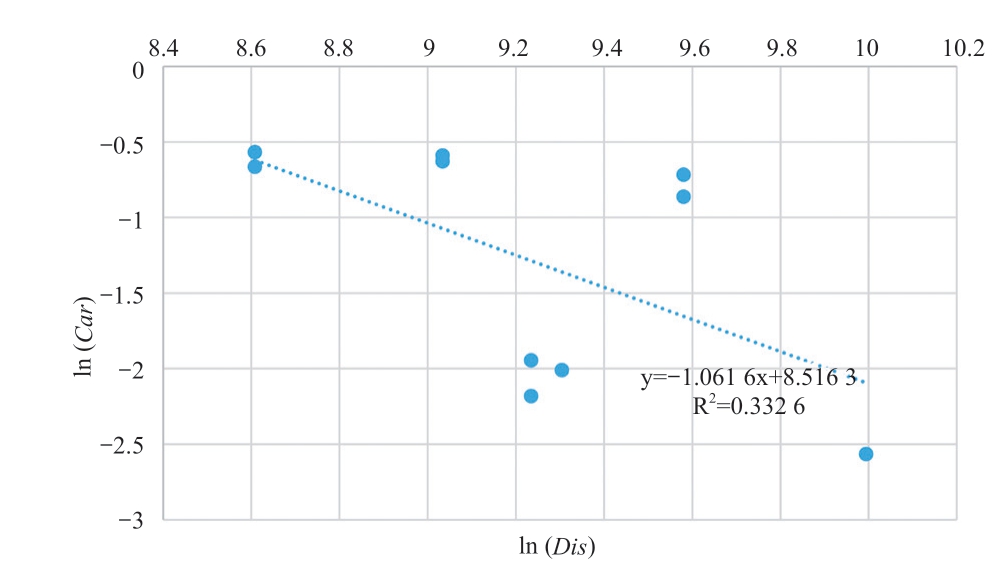
图4 距离衰减指数计算
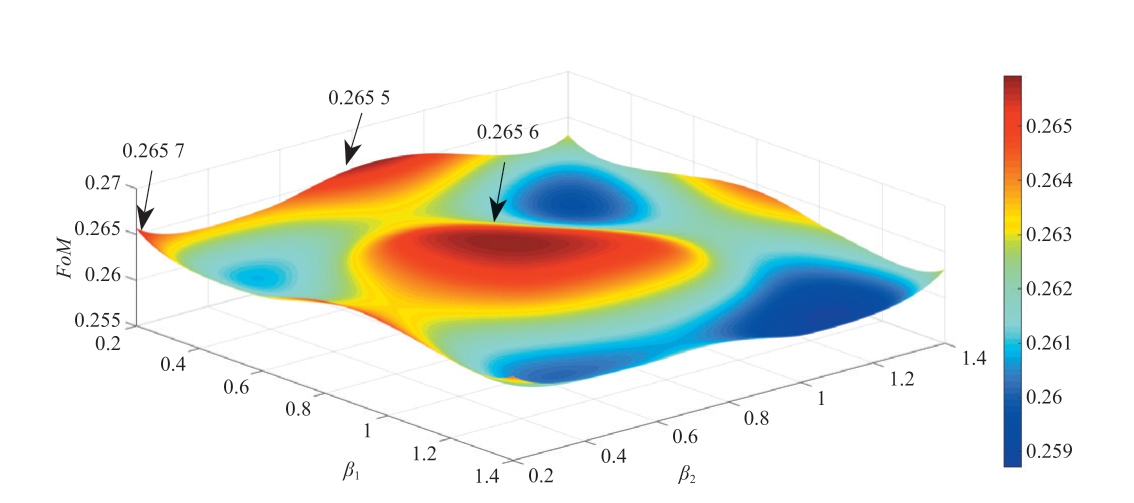
图5 交通可达性模型回归系数敏感性分析
2.3 土地利用模拟结果和精度评价
本研究对深圳市2009—2014 年的土地利用变化进行模拟,得出T-VCA 模型的FoM 模拟精度(表1)和景观指数相似度(表2)。通过对比其他模型,T-VCA 的模拟精度与景观指数相似度最高,分别高达0.266 和96.00%。T-VCA 模拟精度分别较C-VCA、A-VCA、RF-VCA 提高了2.67%、3.75%、11.05%。可见,T-VCA 模型在RF-VCA 基础上考虑到城市连通性和交通可达性的影响,可以更好地挖掘城市土地利用转化规则。
表1 基于不同模型的土地利用模拟结果精度对比
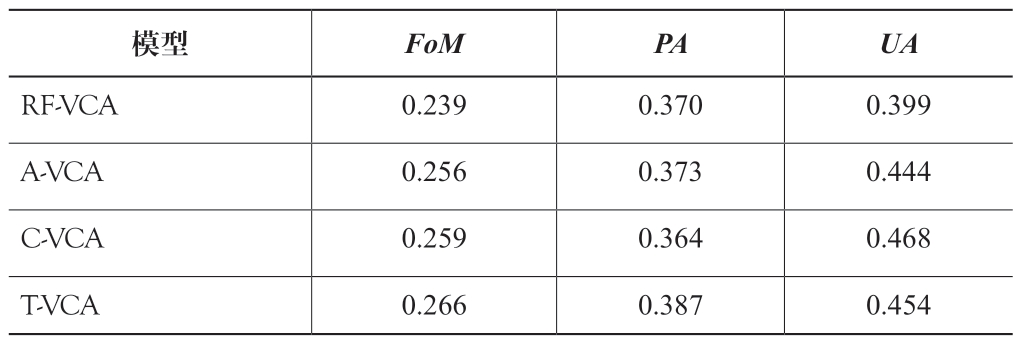
模型FoM PA UA RF-VCA 0.239 0.370 0.399 A-VCA 0.256 0.373 0.444 C-VCA 0.259 0.364 0.468 T-VCA 0.266 0.387 0.454
表2 不同城市发展模拟模型模拟结果的景观指数对比
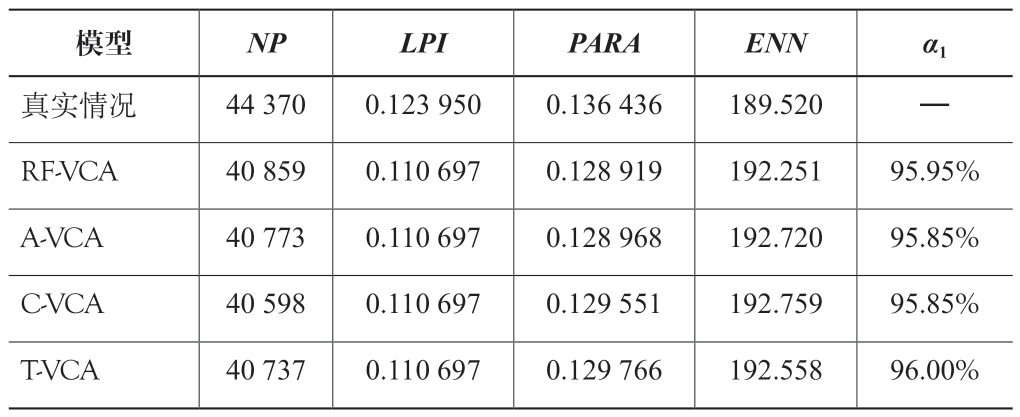
模型NP LPI PARA ENN α1真实情况44 370 0.123 950 0.136 436 189.520—RF-VCA 40 859 0.110 697 0.128 919 192.251 95.95%A-VCA 40 773 0.110 697 0.128 968 192.720 95.85%C-VCA 40 598 0.110 697 0.129 551 192.759 95.85%T-VCA 40 737 0.110 697 0.129 766 192.558 96.00%
通过对比不同城市发展模拟模型模拟的景观指数计算结果可以发现:T-VCA 模型在PARA 指数上与真实地块情况非常接近,景观指数相似度达到了96.00%,高于其他三种模型。与模拟精度FoM 的表现一致,说明T-VCA 模型在城市景观格局模拟上更具优势。
为了探究城市发展模拟的区域差异,研究统计了深圳市不同区县尺度的模拟结果精度(表3)。所提出的T-VCA模型在大鹏新区、光明新区和坪山区等远郊区较其他模型模拟效果更佳,尤其是光明新区模拟精度FoM 达到0.318。C-VCA 模型在各新区的模拟精度均高于A-VCA 模型,但是在福田区、罗湖区等中心城区的模拟精度较低,而A-VCA模型在相应区域的模拟精度却达到了不错的效果,这一现象说明城市交通可达性的空间差异较大,对土地利用变化的影响主要集中在中心城区。值得注意的是,C-VCA 模型与T-VCA 模型在中心城区的模拟精度低于A-VCA 模型,且T-VCA 模型的模拟精度更低;而对于新兴城区和远郊区,T-VCA 模型的模拟精度明显高于其他三种模型。这说明在中心城区,可达性因子对土地扩张具有一定的影响,而连通性因子的引入易干扰模拟精度,同时考虑两项因子将加大对结果的扰动。然而对于新兴城区和远郊区,连通性因子和可达性因子均对土地扩张有影响,且连通性因子影响更为突出,同时考虑两项因子将进一步提高模型的模拟精度。因此,本研究所提出的T-VCA 模型更适用于新兴城区和远郊区的土地利用变化模拟。
表3 深圳市各行政区基于各模型的模拟结果精度FoM 对比
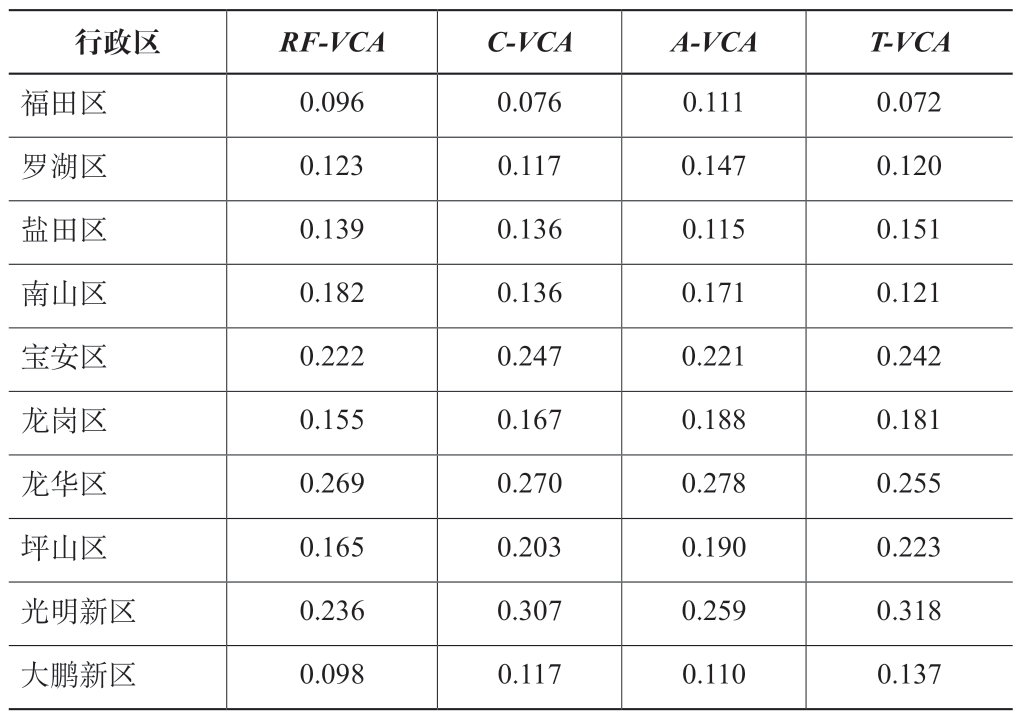
行政区RF-VCA C-VCA A-VCA T-VCA福田区0.096 0.076 0.111 0.072罗湖区0.123 0.117 0.147 0.120盐田区0.139 0.136 0.115 0.151南山区0.182 0.136 0.171 0.121宝安区0.222 0.247 0.221 0.242龙岗区0.155 0.167 0.188 0.181龙华区0.269 0.270 0.278 0.255坪山区0.165 0.203 0.190 0.223光明新区0.236 0.307 0.259 0.318大鹏新区0.098 0.117 0.110 0.137
本研究分别基于RF-VCA、C-VCA、A-VCA 和T-VCA 模拟深圳市2014 年的土地利用格局,展示了中心城区、新兴城区和远郊区等区域的真实和模拟结果(图6)。从不同模型土地利用发展模拟的局部细节图来看,a、b、c 三列细节图中T-VCA 较好模拟出了公共管理服务用地和商业用地,且土地利用格局更接近于实际情况。图7 为不同模型在深圳市各区被正确识别、错误识别的发展地块。被正确模拟的地块主要集中分布在光明新区、宝安区、龙华区等区域交界处,这体现出交界区域城市连通性对城市发展的驱动作用。根据统计,光明新区较宝安区和龙华区具有较高的GDP 增速① 详见http://tjj.sz.gov.cn/。,区域间不同的经济发展水平导致用地发展模式不均衡,模型难以完全挖掘出光明新区大量新增的建设用地。由于福田区、罗湖区等沿海经济发达区域的城区发展更为成熟,导致模型易将发展潜力较小的城市公园或园林错误模拟为建设用地。
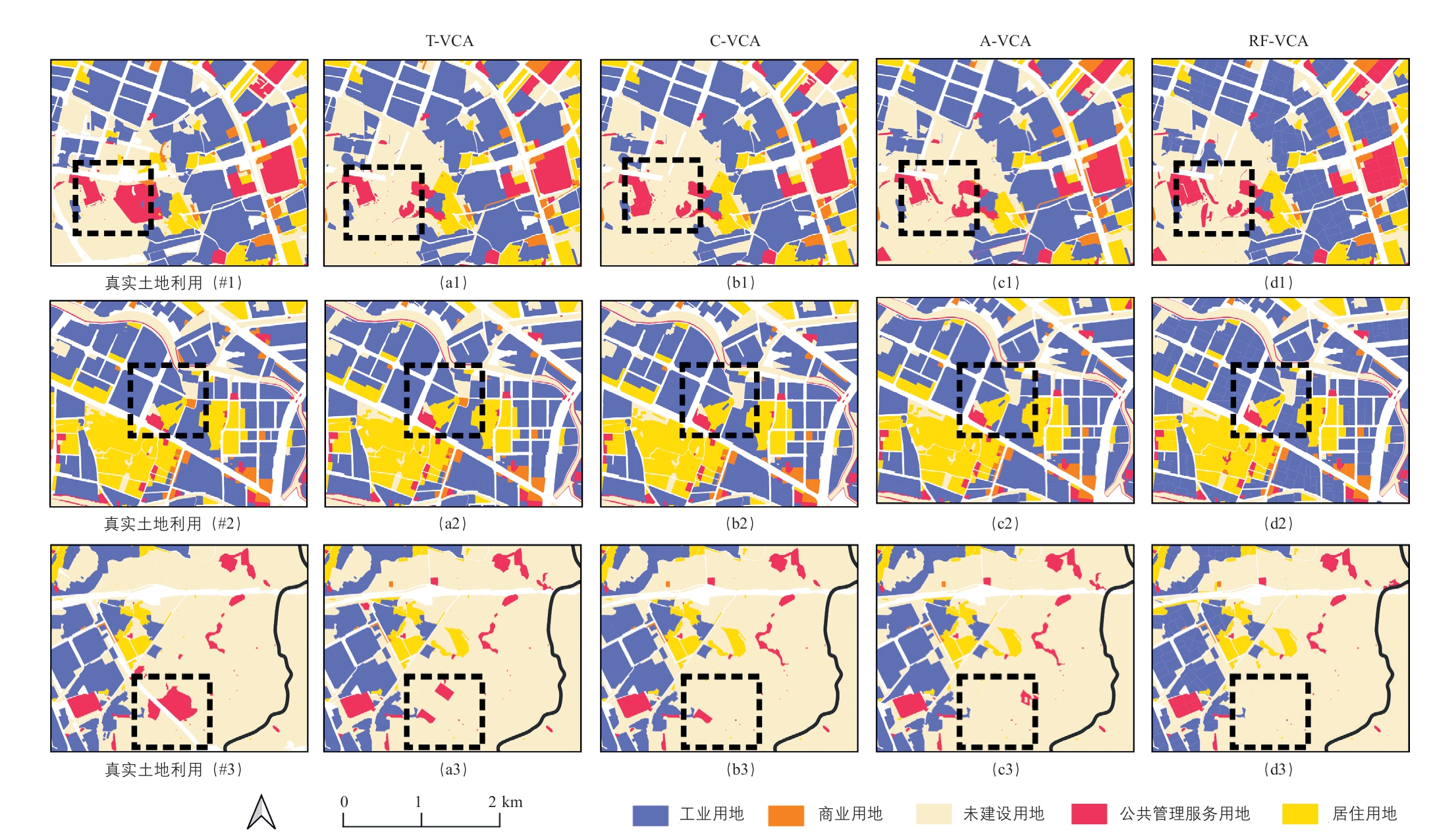
注:a1—a3 采用T-VCA;b1—b3 采用C-VCA;c1—c3 采用A-VCA;d1—d3 采用RF-VCA。
图6 基于不同模型的深圳市局部土地利用发展模拟
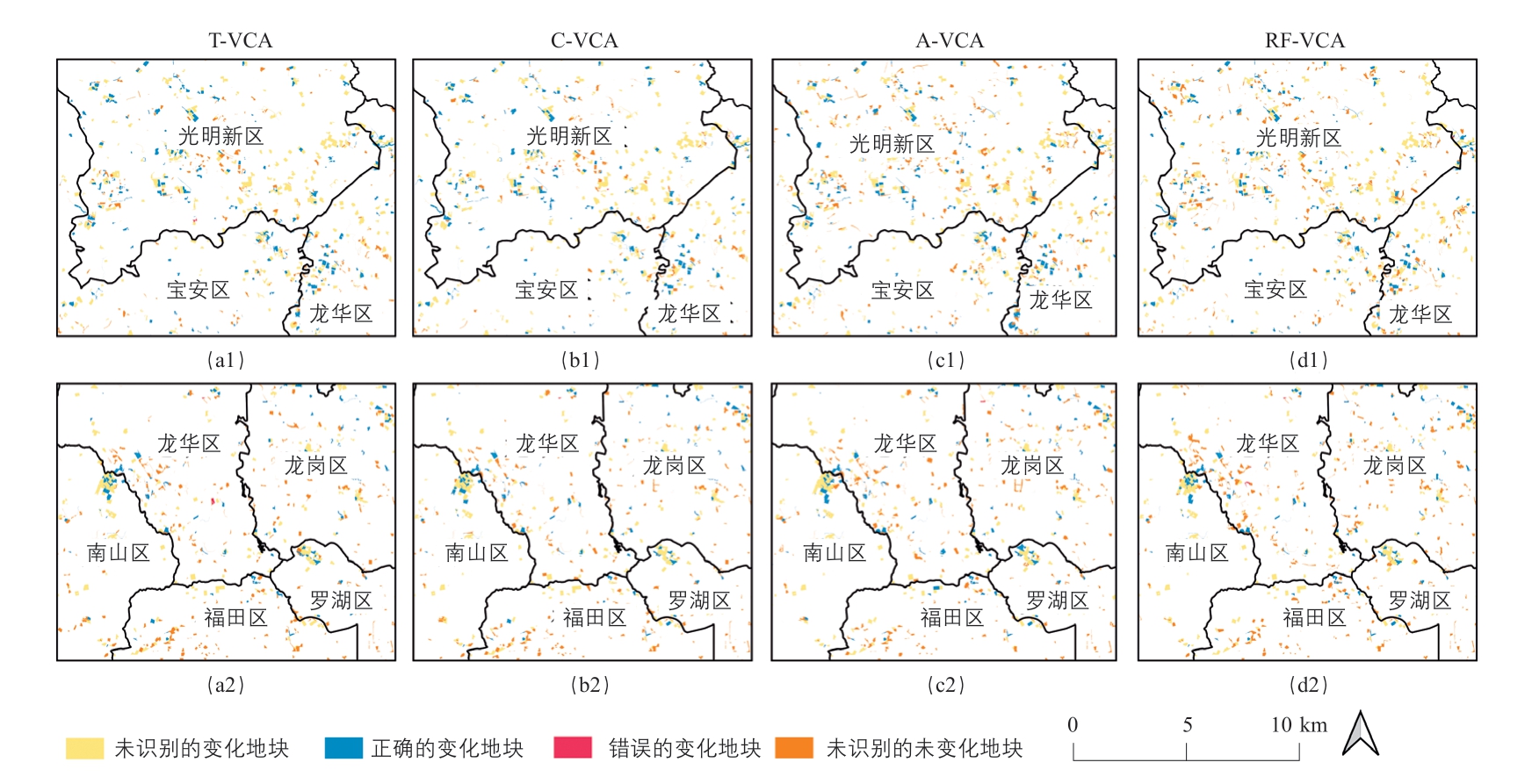
图7 不同模型在深圳市各区被正确识别、错误识别的发展地块
为探究各模型对不同用地类型的模拟特征,研究统计了不同模型对各用地类型地块的模拟正确数量(表4)。A-VCA对公共管理服务用地的模拟效果明显高于C-VCA,考虑到公共管理服务用地主要分布于深圳市中心城区,这一现象也表明A-VCA 更适用于挖掘中心城区的土地利用转化规则。由于中心城区用地接近饱和,新增居住用地主要分布于新兴城区,C-VCA 对居住用地模拟的效果更优,进一步验证其更适用于挖掘新兴城区的土地利用转化规则,这也在一定程度上反映了交通、经济和文化对新兴城区土地利用发展的带动作用。相比于最新的RF-VCA 模型,T-VCA 在工业用地、商业用地和居住用地的模拟上具有明显优势。这说明T-VCA 有效结合了C-VCA 和A-VCA 互补性优点,适用于模拟城市地块尺度的大规模土地利用。
表4 基于不同模型的深圳市各用地类型地块模拟正确的地块数量
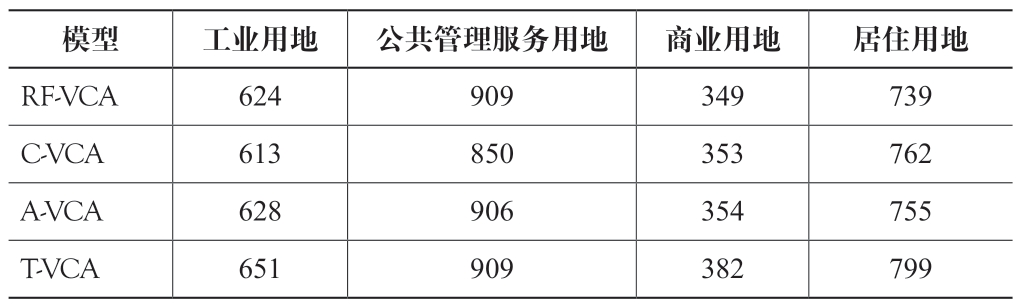
模型工业用地公共管理服务用地商业用地居住用地RF-VCA 624 909 349 739 C-VCA 613 850 353 762 A-VCA 628 906 354 755 T-VCA 651 909 382 799
3 讨论
考虑交通因素对城市土地利用模拟的影响,本研究创新性地提出了考虑交通驱动因素的城市发展模拟模型T-VCA。通过设置C-VCA、A-VCA 和RF-VCA 三个模型作为对比实验,定量证实了考虑交通因素可以有效挖掘城市土地类型转化规则。其中,C-VCA 模型模拟精度较A-VCA 模型提高了1.05%,表明连通性因子可以体现城市各区域之间的关联性和凝聚力,更好地模拟景观分布的连续性特征。
通过分析模型对各城区的模拟精度和对不同用地类型地块发展变化的模拟结果,发现A-VCA 在发展较为成熟的中心城区实现了最佳模拟精度,更适用于挖掘中心城区的土地利用转化规则;C-VCA 优先考虑路网对沿线土地利用变化的影响,更适用于挖掘新兴城区和远郊区的土地利用转化规则;T-VCA 同时考虑城市连通性和交通可达性因素,有效结合C-VCA 和A-VCA 的优势,最大程度顾及新兴城区和远郊区在交通等因素作用下的土地地块发展相关性,从而达到了最佳的模拟效果。因此在城市发展模拟中,结合区域自身发展特征和模型优势选取相应的VCA 模型,可以有效提高模拟结果精度。在城市未来规划过程中,可结合交通可达性和城市连通性特点,根据区域建设的发展程度对城市交通、经济和文化等资源进行合理配置,以促进城市发展。
参数设置和计算可以直接影响模型的精度,敏感性分析中β1、β2 两个重要参数的调节过程中出现了有趣的现象。结果显示当回归系数取值较小时,交通可达性作用范围主要集中于交通主干道附近区域,该范围内城市的空间聚集程度较高,因此出现了第一个“波峰”;随着回归系数增大,地块与道路的距离对交通可达性影响增强,交通可达性作用范围增大,进而提高对城市中心区域的模拟精度,形成第二个“波峰”;当回归系数继续增加,更加突出了郊区受交通可达性的影响,使得模型对靠近郊区的潜在城市中心的模拟精度提升,形成第三个“波峰”。但由于距离衰减效应的影响,整体模拟精度随作用范围扩大呈递减趋势。
另外,本研究还存在一些不足。随着交通需求的增加,城市路网不断扩张完善,仅以特定年份静态的交通路网空间分布进行模拟存在一定的局限性。因此,如何引入城市交通规划政策和未来交通路网发展来提高未来模拟的效果可作为今后的研究方向之一。此外,未来将考虑预测城市土地利用变化,并引入置信区间量化土地利用类型的转化概率,以提高模型的可靠性。
4 结论
交通是城市发展的重要支撑,对城市的发展规模和土地利用格局具有决定性作用。针对城市土地利用模拟中交通驱动因素考虑不足的问题,本研究提出了一套考虑交通因素的城市土地利用变化模拟框架(T-VCA),能够有效模拟微观地块尺度的城市土地利用变化。在不同模型对城市发展进行模拟的对照实验中,T-VCA 模型具有最高的FoM 精度(0.266)和景观指数相似度(96.00%),表明T-VCA 对城市土地利用格局的模拟能力更为出色。城市交通因素对城市用地的规模、空间交互强度以及空间分布变化具有不同程度的影响,基于出租车轨迹、城市经济和文化的城市连通性因素适用于挖掘新兴城区和远郊区的土地利用转化规则,而基于城市路网分布的城市交通可达性因素适用于挖掘发展成熟的中心城区的土地利用转化规则。
因此,在深圳市中心区域采用考虑交通可达性因子的A-VCA 模型,在新兴城区和远郊区采用考虑城市连通性因子和交通可达性因子的T-VCA 模型,可以更为有效地模拟大规模的土地利用地块变化。未来研究可根据区域发展程度,动态引入城市连通性因子和交通可达性因子,并考虑长距和短距通勤对城市发展的作用,进一步提高模拟精度和模型适用性,为城市规划工作者提供实用信息。
注:文中未注明资料来源的图表均为作者绘制。
[1] YUAN Y, ZHAO T, WANG W, et al. Projection of the spatially explicit land use/cover changes in China, 2010-2100[J]. Advances in meteorology,2013(2/3): 1-9.
[2] ALMEIDA C M, GLERIANI J M, CASTEJON E F, et al. Using neural networks and cellular automata for modelling intra-urban land-use dynamics[J]. International journal of geographical information science: 2008,22(9): 943-963.
[3] DENG J S, WANG K, HONG Y, et al. Spatio-temporal dynamics and evolution of land use change and landscape pattern in response to rapid urbanization[J]. Landscape and urban planning, 2009, 92(3/4): 187-198.
[4] DADASHPOOR H, AZIZI P, MOGHADASI M. Land use change,urbanization, and change in landscape pattern in a metropolitan area[J].Science of the total environment, 2019, 655: 707-719.
[5] GU W, GUO J, FAN K, et al. Dynamic land use change and sustainable urban development in a third-tier city within Yangtze Delta[J]. Procedia environmental sciences, 2016, 36: 98-105.
[6] 王家丰, 王蓉, 冯永玖, 等. 顾及轨道交通影响的浙中城市群土地利用多情景模拟与分析[J]. 地球信息科学学报, 2020, 22(3): 605-615.
[7] BATTY M. Urban evolution on the desktop: simulation with the use of extended cellular automata[J]. Environment and planning a, 1998, 30(11):1943-1967.
[8] LI X, CHEN Y, LIU X, et al. Experiences and issues of using cellular automata for assisting urban and regional planning in China[J].International journal of geographical information science, 2017, 31(8): 1606-1629.
[9] LI X, YEH A G. Neural-network-based cellular automata for simulating multiple land use changes using GIS[J]. International journal of geographical information science, 2002, 16(4): 323-343.
[10] LIU X, MA L, LI X, et al. Simulating urban growth by integrating landscape expansion index (LEI) and cellular automata[J]. International journal of geographical information science, 2014, 28(1): 148-163.
[11] LIU X, LIANG X, LI X, et al. A future land use simulation model (FLUS)for simulating multiple land use scenarios by coupling human and natural effects[J]. Landscape and urban planning, 2017, 168: 94-116.
[12] BARREIRA-GONZÁLEZ P, GÓMEZ-DELGADO M, AGUILERABENAVENTE F. From raster to vector cellular automata models: a new approach to simulate urban growth with the help of graph theory[J].Computers, environment and urban systems, 2015, 54: 119-131.
[13] STEVENS D, DRAGIĆEVIĆ S. A GIS-based irregular cellular automata model of land-use change[J]. Environment and planning b: planning and design, 2007, 34(4): 708-724.
[14] O’SULLIVAN D. Exploring spatial process dynamics using irregular cellular automaton models[J]. Geographical analysis, 2001, 33(1): 1-18.
[15] MORENO N, MÉNARD A, MARCEAU D J. VecGCA: a vector-based geographic cellular automata model allowing geometric transformations of objects[J]. Environment and planning b: planning and design, 2008, 35(4):647-665.
[16] SEMBOLONI F. The growth of an urban cluster into a dynamic selfmodifying spatial pattern[J]. Environment and planning b, planning and design, 2000, 27(4): 549-564.
[17] NORTE PINTO N, PAIS ANTUNES A. A cellular automata model based on irregular cells: application to small urban areas[J]. Environment and planning b: planning and design, 2010, 37(6): 1095-1114.
[18] YAO Y, LIU X, LI X, et al. Simulating urban land-use changes at a large scale by integrating dynamic land parcel subdivision and vector-based cellular automata[J]. International journal of geographical information science, 2017,31(12): 2452-2479.
[19] JJUMBA A, DRAGIĆEVIĆ S. High resolution urban land-use change modeling: Agent iCity approach[J]. Applied spatial analysis and policy, 2012,5(4): 291-315.
[20] 于茜, 白建军, 张晶言, 等. 路网通达性与城镇空间扩展的耦合关系——以西安市为例[J]. 经济地理, 2016, 36(10): 69-75.
[21] HE L, LIU Y, H Q, et al. Simulating urban cooperative expansion in a single-core metropolitan region based on improved CA model integrated information flow: case study of Wuhan urban agglomeration in China[J].Journal of urban planning and development, 2018, 144(2): 05018002.
[22] YU Y, HE J, TANG W, et al. Modeling urban collaborative growth dynamics using a multiscale simulation model for the Wuhan urban agglomeration area,China[J]. ISPRS international journal of geo-information, 2018, 7(5): 176.
[23] FOTHERINGHAM A S. Spatial structure and distance-decay parameters[J].Annals of the Association of American Geographers, 1981, 71(3): 425-436.
[24] 张童, 姚士谋, 胡伟平, 等. 基于交通可达性的广佛都市区城市扩展的模拟与分析[J]. 地理科学, 2018, 38(5): 737-746.
[25] ZHU J, ZHENG J, DI S, et al. Cellular automata based land-use change simulation considering spatio-temporal influence heterogeneity of light rail transit construction: a case in Nanjing, China[J]. ISPRS international journal of geo-information, 2021, 10(5): 308.
[26] ALJOUFIE M, ZUIDGEEST M, BRUSSEL M, et al. A cellular automatabased land use and transport interaction model applied to Jeddah, Saudi Arabia[J]. Landscape and urban planning, 2013, 112: 89-99.
[27] HE C, ZHAO Y, TIAN J, et al. Modeling the urban landscape dynamics in a megalopolitan cluster area by incorporating a gravitational field model with cellular automata[J]. Landscape and urban planning, 2013, 113: 78-89.
[28] LIANG S. Research on the urban influence domains in China[J].International journal of geographical information science, 2009, 23(12):1527-1539.
[29] JINGHU P, WEISHENG L. Quantitative delimitation of urban influential hinterland in China[J]. Journal of urban planning and development, 2015,141(4): 04014033.
[30] LV J, WANG Y, LIANG X, et al. Simulating urban expansion by incorporating an integrated gravitational field model into a demand-driven random forest-cellular automata model[J]. Cities, 2021, 109: 103044.
[31] XIAO Y, WANG F, LIU Y, et al. Reconstructing gravitational attractions of major cities in China from air passenger flow data, 2001-2008: a particle swarm optimization approach[J]. The professional geographer, 2013, 65(2):265-282.
[32] WOLD S, ESBENSEN K, GELADI P. Principal component analysis[J].Chemometrics and intelligent laboratory systems, 1987, 2(1/3): 37-52.
[33] STOICA I, TULLA A F, ZAMFIR D, et al. Exploring the urban strength of small towns in Romania[J]. Social indicators research, 2020, 152(3): 843-875.
[34] TOBLER W R. A computer movie simulating urban growth in the Detroit region[J]. Economic geography, 1970, 46(Supplement 1): 234-240.
[35] PINTO N, ANTUNES A O N P, ROCA J. A cellular automata model for integrated simulation of land use and transport interactions[J]. ISPRS international journal of geo-information, 2021, 10(3): 149.
[36] NAVARRO CERRILLO R M, PALACIOS RODR I GUEZ G, CLAVERO RUMBAO I, et al. Modeling major rural land-use changes using the GISbased cellular automata metronamica model: the case of Andalusia (Southern Spain)[J]. ISPRS international journal of geo-information, 2020, 9(7): 458.
[37] ZHAO L, SHEN L. The impacts of rail transit on future urban land use development: a case study in Wuhan, China[J]. Transport policy, 2019, 81:396-405.
[38] PONTIUS R G, BOERSMA W, CASTELLA J, et al. Comparing the input,output, and validation maps for several models of land change[J]. The annals of regional science, 2008, 42(1): 11-37.
[39] ZHUANG H, LIU X, YAN Y, et al. Integrating a deep forest algorithm with vector-based cellular automata for urban land change simulation[J].Transactions in GIS, 26, 2056-2080. https://doi.org/10.1111/tgis.12935.
[40] ZHAI Y, YAO Y, GUAN Q, et al. Simulating urban land use change by integrating a convolutional neural network with vector-based cellular automata[J]. International journal of geographical information science,2020, 34(7): 1475-1499.
[41] HEUVELINK G B. Error propagation in environmental modelling with GIS[M]. New York: CRC Press, 1998.
[42] FENG Y, TONG X. A new cellular automata framework of urban growth modeling by incorporating statistical and heuristic methods[J]. International journal of geographical information science, 2020, 34(1): 74-97.
[43] YAO Y, LI X, LIU X, et al. Sensing spatial distribution of urban land use by integrating points-of-interest and Google Word2Vec model[J]. International journal of geographical information science, 2016, 31(4): 825-848.
[44] YAO Y, LIU X, LI X, et al. Simulating urban land-use changes at a large scale by integrating dynamic land parcel subdivision and vector-based cellular automata[J]. International journal of geographical information science, 2017,31(12): 2452-2479.
[45] CHEN J, CHANG K, KARACSONYI D, et al. Comparing urban land expansion and its driving factors in Shenzhen and Dongguan, China[J].Habitat international, 2014, 43: 61-71.
[46] WAND M P, JONES M C. Kernel smoothing[M]. New York: CRC Press,1994.
[47] YUAN J, ZHENG Y, XIE X. Discovering regions of different functions in a city using human mobility and POIs(DRoF)[C] // The 18th SIGKDD conference on knowledge discovery and data mining. ACM, 2012.
[48] LI S, ZHUANG C, TAN Z, et al. Inferring the trip purposes and uncovering spatio-temporal activity patterns from dockless shared bike dataset in Shenzhen, China[J]. Journal of transport geography, 2021, 91: 102974.
[49] LIU Y, WANG F, KANG C, et al. Analyzing relatedness by Toponym Co-Occurrences on web pages[J]. Transactions in GIS, 2014, 18(1): 89-107.
