引言
随着中国城镇化进程的加快,人口、空间、生产与消费资料高度集中,超高密度、快速高频率的人群动态集聚成为中国特大城市的突出特征。海量人群在城市中的动态时空运动在驱动城市经济活动发展的同时,也产生了人与空间之间的冲突,交通拥堵[1]、环境污染[2]、设施错配[3]、“鬼城”“卧城”[4]等一系列城市问题不断暴露出来。基于时空大数据实现城市的精细化洞察和预测成为解决以上问题的关键之一[5]:通过解析人群活动规律特征,剖析潜在城市问题,制定相应的城市政策来调整城市建设,使城市建成环境更好地满足和适应城市人群的活动需求。
自1950 年代克拉克(Clark)提出城市人口密度模型以来[6],城市人群的空间分布模型和规律一直是城市研究的重要议题。例如:国土空间规划编制着重研究大尺度的、相对静态的人地关系,针对人口密度的空间分布,结合生态适应性要求进行有效疏解或结合人口规模比例提出相应的产业和基础设施部署[7];片区级的空间规划则倾向于研究小尺度的、更加动态的人地关系,结合人群活动类型与流线[8],改善空间环境或进行人流仿真,测试拥堵情况,以适应大型活动或事件的疏散需求,从而规避风险[9]。因此,建构动态人群时空分布预测模型,模拟人群时空变化情况,是规划学科有效解决和规避城市问题,提高城市空间品质的重要抓手。
传统的城市人群分布模型构建方法主要基于统计学,采用指数函数、二项式函数、正态分布函数等,能够对不同类型城市人群分布进行总体描述,但限于数据精度,难以进行精细化的模拟和验证。2010 年以来,随着手机等移动定位设备和信息技术的完善,借助时空大数据能够进行城市海量人群分布的检测,于是建构精细化的城市人群分布模型成为可能[10-11]。尤其是深度学习等前沿算法的引入,能够较好地解决城市人群复杂性问题,使隐藏在城市海量人群动态分布数据中的规律能够被进一步挖掘。巴蒂(Batty)认为,城市是由人流、车流和信息流等不同的流组成的可计算的复杂网络体,利用城市计算模型可以辅助洞察城市规律和优化城市治理[12]。卢卡等(Luca et al.)指出了城市人群动态分布的传统模型建构方法的局限[13],并提出基于深度学习的城市人群动态位置模拟的测算方法[14]。还有学者开发了基于半监督学习模型的城市人群动态分布算法,并使用多个公共真实数据集进行了验证[15]。吴志强提出,将时空大数据与智能技术相结合,构建城市量化模型并推演人群时空分布,将是未来城市规划的十项重点技术方向之首[16]。
本文基于手机信令大数据和城市建成环境数据,利用卷积神经网络(CNN: Convolutional Neural Network)模型构建了人群时空密度预测模型框架,在此基础上集成32 个关键建成环境特征指标形成指标库,测算南京24 小时的人群动态分布状况,并对模型的准确率进行整体评价和误差检验。笔者希望通过探索城市人群动态模型建构方法,提升城市人群时空分布测算的准确性,为城市规划管理和建设决策提供科学依据和指引。
1 模型构建方法
卷积神经网络作为一种经典的深度学习模型,在计算机视觉领域得到了广泛的应用,在图像分类问题上的表现明显优于传统方法。与其他深度学习方法相比,卷积神经网络模型在特征提取方面有两个优点。(1)卷积层中的每一层仅链接上一层的输入神经元的一部分,卷积核的尺寸远小于输入数据的尺寸,因而能降低计算复杂度,提高运算效率。卷积运算采用对应相乘的方法获得特征图,该方法能够更有效地从图像中提取特征。(2)引入了一种被称为池化层的操作机制,能极大减少模型参数的数量,降低模型的训练难度,提高模型的运算效率[17]。
本研究将人群时空分布和建成环境特征转化为图像,从而将序列性预测问题转换为图的预测问题,因此可以有效利用卷积神经网络方法。在模型建构方面,卷积神经网络方法具有以下优点:(1)采用卷积层和池化层,可以自动提取建成环境特征因子,避免了主观选择特征因子可能导致的遗漏和重复问题;(2)卷积层的运算方法可以有效处理空间相关问题,将空间自相关纳入建模范畴,而池化层显著提高了模型的运算效率,可以应用于分析解决大规模的城市尺度上的问题。考虑到深度学习中随着网络层数的加深会造成过度拟合和梯度消失的问题,最终采用卷积神经网络中的深度残差网络(ResNet)应用于本研究的模型构建。深度残差网络采用跨层链接的思想,通过捷径链接的方法,能够较好解决随着网络层数的加深造成的准确率下降问题。
模型以建成环境因子作为自变量,以工作日的人群时空分布情况(人群密度)作为因变量。首先构建人群多时段密度与建成环境因子的特征数据集,再将经标准化处理的数据输入模型,通过模型训练的方式,对模型进行迭代和优化。模型构建包括以下四个步骤:数据对的处理与构建、数据集的构建与划分、模型构建、模型训练与输出。本研究构建了包含32 个建成环境因子和人群时空密度分布特征的数据库,并选择深度残差网络构建卷积神经网络模型,以完成对南京市人群时空分布的模拟(图1)。
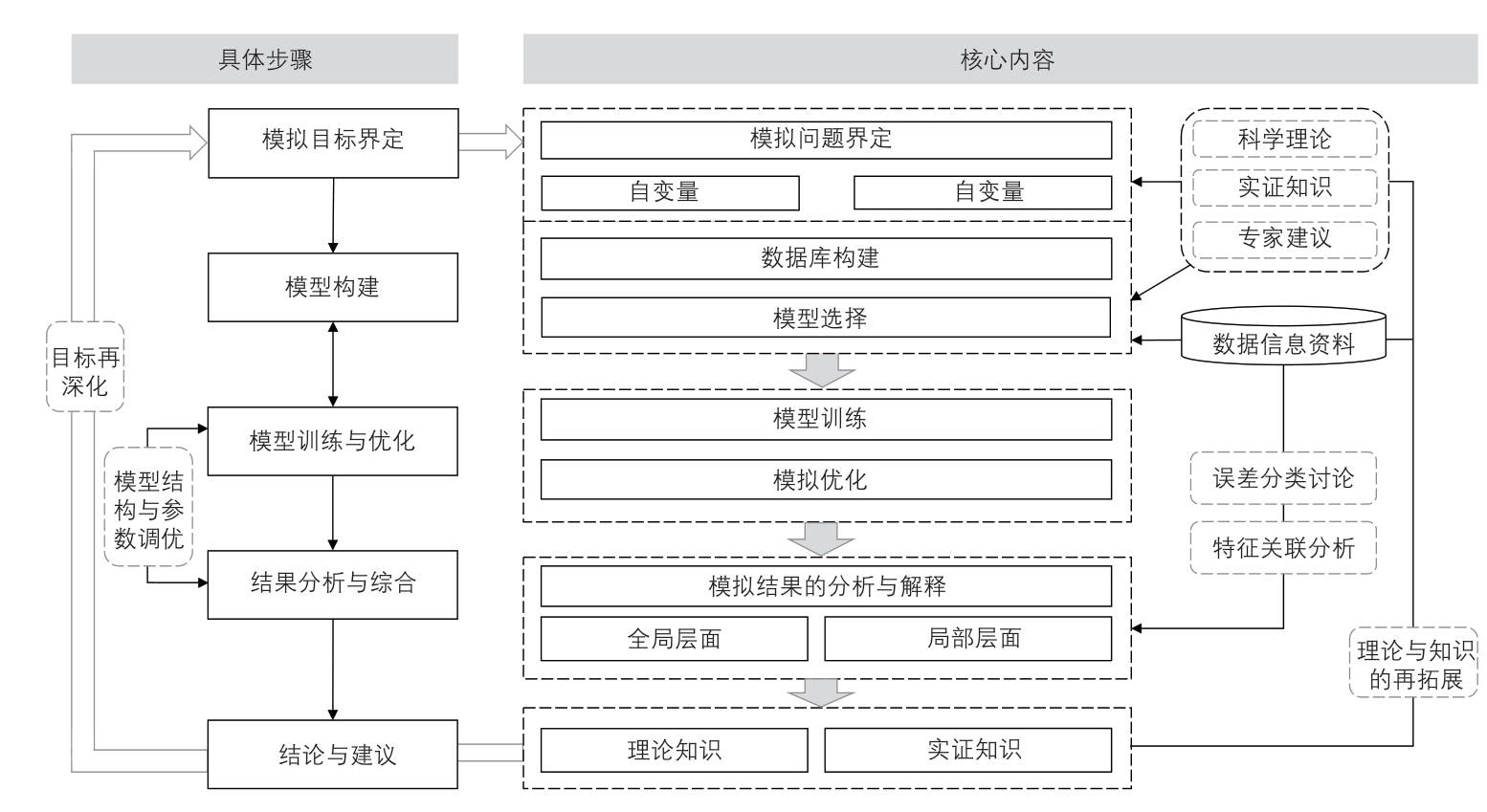
图1 数据驱动的基于建成环境的人群密度时空分布预测模型框架
2 数据来源与处理方法
2.1 研究案例与数据来源
本文选取南京市为研究范围,按照《南京市城市总体规划(2011—2020)》将南京市域划分为老城、主城区、中心城区和市域四个圈层进行分类研究(图2),并采用500 m×500 m 的矩形栅格作为空间分析单元。
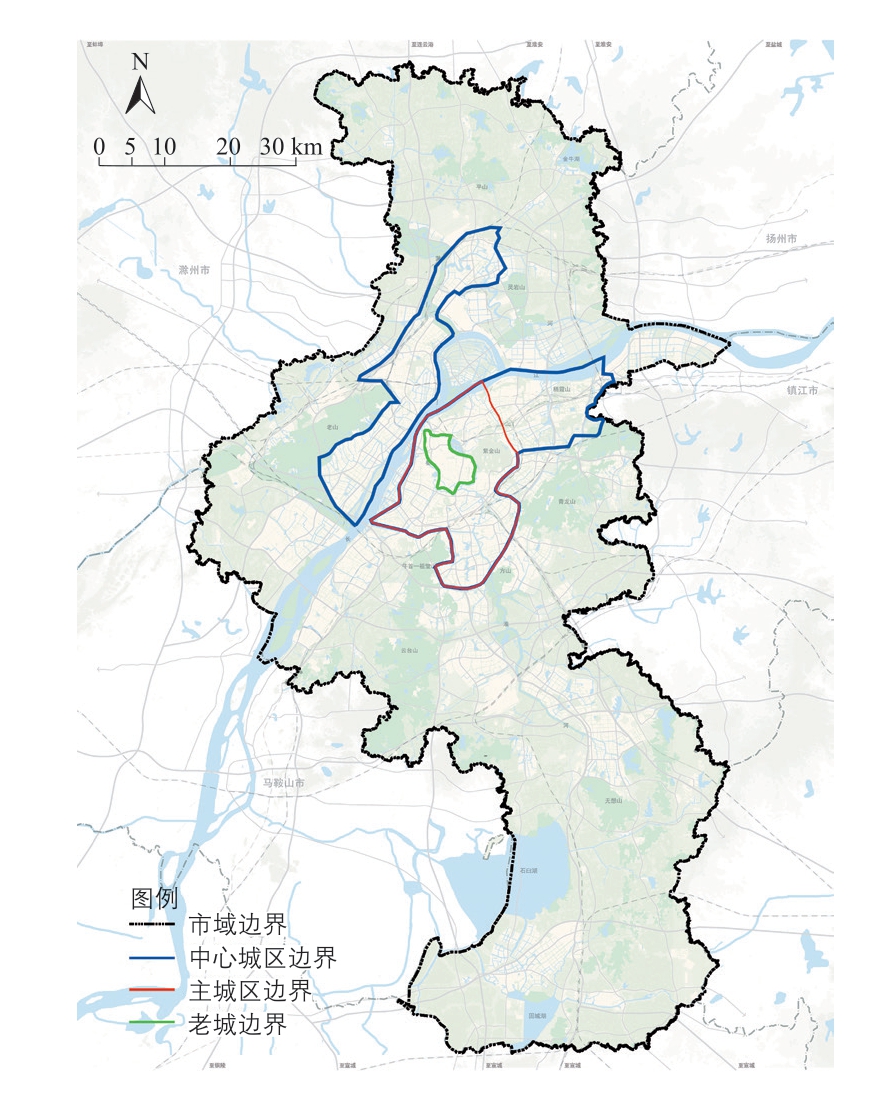
图2 南京市研究范围圈层划分
人群时空分布数据基于中国移动提供的南京市域范围内匿名手机信令数据,时间范围为2015年11月连续5个工作日。经数据清洗后,每日手机用户量约500 万,人均空间记录36条。数据包含四个字段:用户ID、对应基站编号、位置时间戳,以及对应基站的经纬度坐标(表1)。
表1 手机信令数据示例表
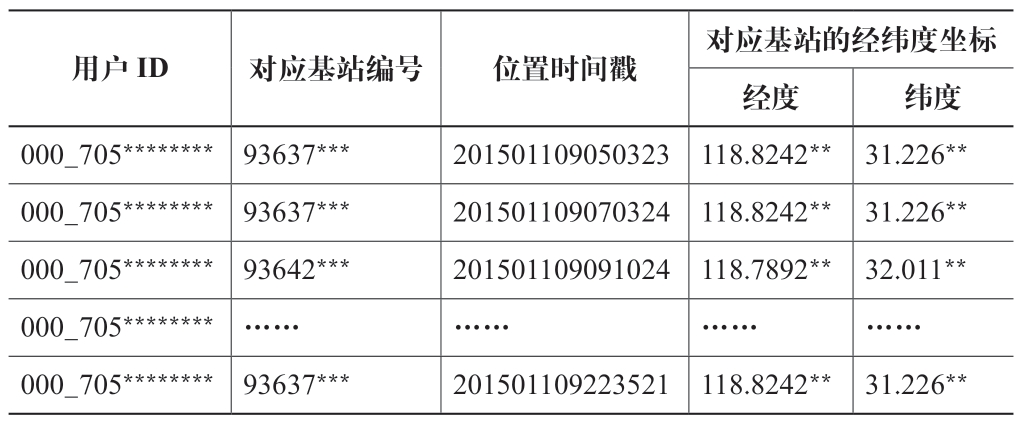
用户ID对应基站编号位置时间戳对应基站的经纬度坐标经度纬度000_705******** 93637***201501109050323 118.8242** 31.226**000_705******** 93637***201501109070324 118.8242** 31.226**000_705******** 93642***201501109091024 118.7892** 32.011**000_705******** ……………………000_705******** 93637***201501109223521 118.8242** 31.226**
建成环境数据包括土地利用、建筑形态、道路交通和业态POI 数据。其中,土地利用、建筑形态和道路交通数据基于测绘地形数据,业态POI 数据基于高德地图应用程序编程接口(API)平台获取,并经抽样实地踏勘验证。
2.2 处理方法
(1)人群时空密度分布数据处理。对于人群时空密度分布数据集,本研究的训练目标涉及24 个连续的时间序列,因此需要对其输出标签进行处理,具体方法如下。
对每一个空间分析单元k,生成指定任意网格的人群时空密度分布序列![]()
![]() 为第k 个网格在t 时刻人群时空密度的演变标签。
为第k 个网格在t 时刻人群时空密度的演变标签。
模型训练阶段,为提升机器学习的效率,本文利用主成分分析法(PCA)对24 小时的人群密度分布数据进行降维处理(Nprim 表示提取主成分的数量)。在模型输出环节中,再通过对主成分的反变换,重新得到24 小时的人群密度演化结果。经计算,当Nprim=6 时主成分能解释98.7%的方差,因此取经过主成分分析降维后按方差占比降序排序的前6 个主成分作为降维后的特征标签,降维后的人群时空密度分布的输出标签记作yPCA。
(2)建成环境因子筛选。分区位、用地结构、空间容量、交通设施、功能业态五方面设置因子,可能与人群时空分布相关的因子共计40 个(表2)。对建成环境因子进行量化处理,为使各因子具有可比性,使用Z-score 标准化方法去除量纲影响,将各因子数据按比例缩放,落入均值为0、标准差为1 的区间。
表2 建成环境因子汇总表
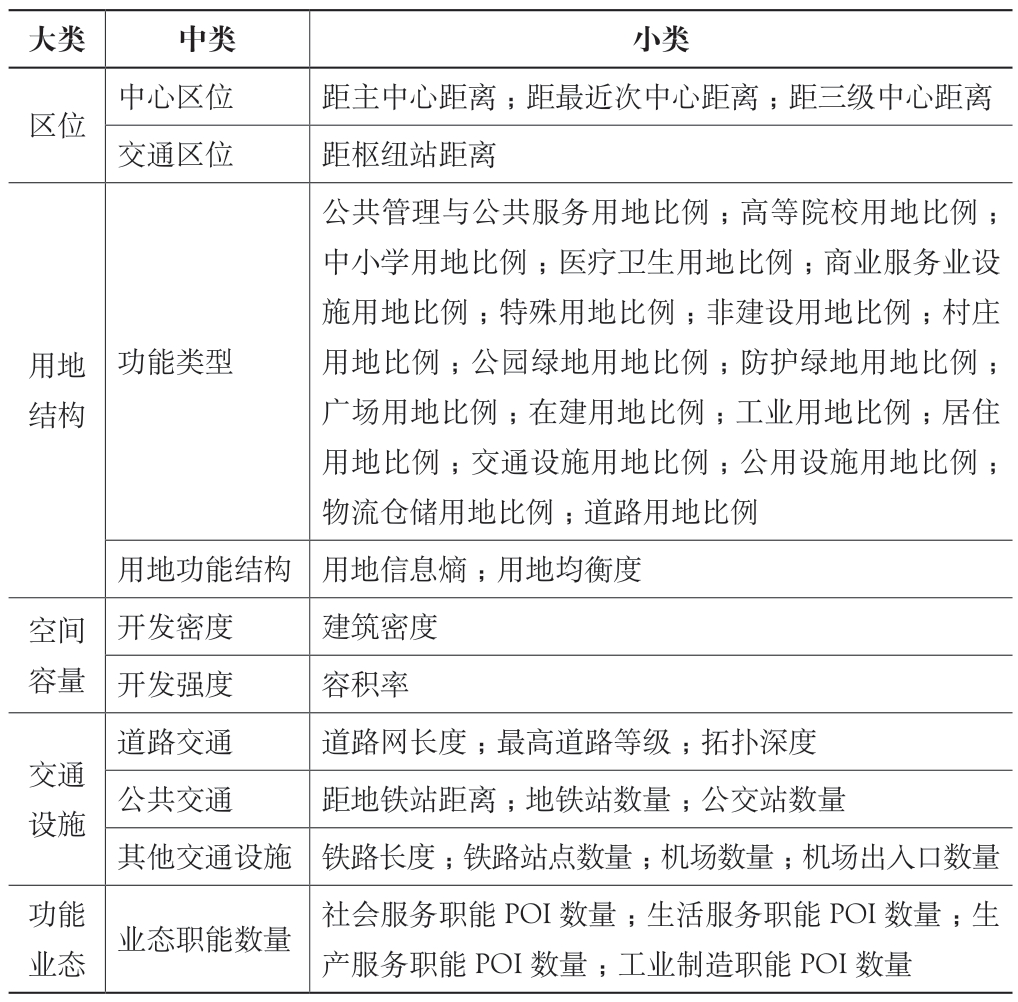
大类中类小类区位中心区位距主中心距离;距最近次中心距离;距三级中心距离交通区位距枢纽站距离用地结构功能类型公共管理与公共服务用地比例;高等院校用地比例;中小学用地比例;医疗卫生用地比例;商业服务业设施用地比例;特殊用地比例;非建设用地比例;村庄用地比例;公园绿地用地比例;防护绿地用地比例;广场用地比例;在建用地比例;工业用地比例;居住用地比例;交通设施用地比例;公用设施用地比例;物流仓储用地比例;道路用地比例用地功能结构 用地信息熵;用地均衡度空间容量开发密度建筑密度开发强度容积率交通设施道路交通道路网长度;最高道路等级;拓扑深度公共交通距地铁站距离;地铁站数量;公交站数量其他交通设施 铁路长度;铁路站点数量;机场数量;机场出入口数量功能业态业态职能数量社会服务职能POI 数量;生活服务职能POI 数量;生产服务职能POI 数量;工业制造职能POI 数量
为提升算法性能,采用过滤式(filter)方法,使用皮尔森相关系数对因子进行特征选择。将40 个建成环境因子的特征值与经过主成分降维后的人群时空密度分布特征标签值做相关性分析,且只要建成环境特征与经过主成分降维后的6 个因子值中有一维相关性(相关性绝对值大于0.1),同时p 值能通过0.05 的显著性检验,则将该建成环境特征纳入训练范畴。40 个因子中有37 个的皮尔森系数通过相关性检验,前32 个变量的相关系数大于0.1,予以选择和保留,作为模型构建中的建成环境因子。
此外,根据地理学第一定律,临近的地理空间很大概率具有相似的地理环境与人群密度分布,而具有相似地理环境特征的不相邻区域也可能具有相似的人群密度分布。因此在预测特征构建时,空间临近区域的建成环境情况也被纳入考虑范围。具体做法为将网格及其周边共(2h+1)2 个网格的建成环境特征一并纳入考虑范畴,即以某一空间单元为中心,四周与之毗连的h 个空间单元所共同覆盖的方形区域。本次研究取h=5,从图3 可以明显看出,周边区域建成环境特征图像的相关性大于0.6,呈现一定的圈层递减模式,这与地理学的相关假设一致。
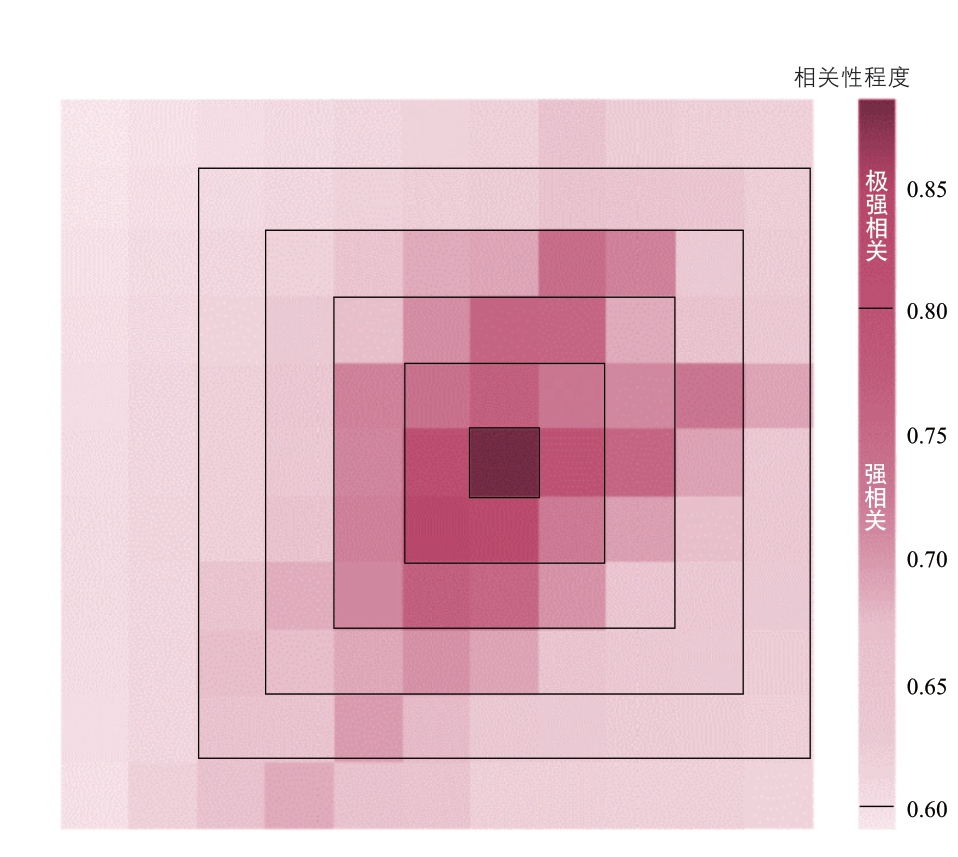
图3 h=5 时的建成环境空间相关性分布
(3)输入特征数据对的构建。基于上述人群时空密度与建成环境因子筛选,得到具有统一格式的输入特征数据对(x,yPCA)。对于空间分析单元i,输入的建成环境特征Xi 是一个三维数组,第一维表示该空间建成环境因子,第二、三维表示一个空间分析单元与其周围建成环境因子的平面分布,即空间分析单元以及与其相邻的(2h+1)2-1 个空间分析单元的数据,本文选h=5。训练数据对为(x,yPCA),对于训练结果yPCA,可通过主成分分析反变换得到24 小时的人群演化模拟结果Y={y[0],y[1],y[2],…,y[23]}。通过该步骤,每个空间分析单元在模型计算中都会带动与其相邻的120 个空间分析单元共同进行训练,保证数据模型的稳定性。
(4)数据集筛选与划分。基于城市的实际状况和模拟方法特性,对现状人群时空密度与建成环境组成的数据对的集进行进一步筛选和划分。现状各空间分析单元日平均人数分布均值呈现幂律分布特征,20%的空间栅格占据了80%以上的人流量,而剩余的80%网格的用地几乎全部以非建设用地为主。日平均人群数量小于200 人的空间分析单元共9 210 个,占比73.56%。若直接使用所有空间分析单元的数据来训练模型,结果会严重倾斜于人群较少的空间分析单元,从而造成较大的误差。因此,本文采用分类针对性学习的方法将数据样本分为两类进行训练,实际日均人群数量小于200 人的记为分类区间0,大于200 人的记为分类区间1。可以看出日均人群数量小于200 人的空间分析单元大多分布于城市郊区,大于200 人的空间分析单元则主要分布于中心城区内(图4)。此步骤消除了大量非建设区对模型计算结果可能产生的干扰。
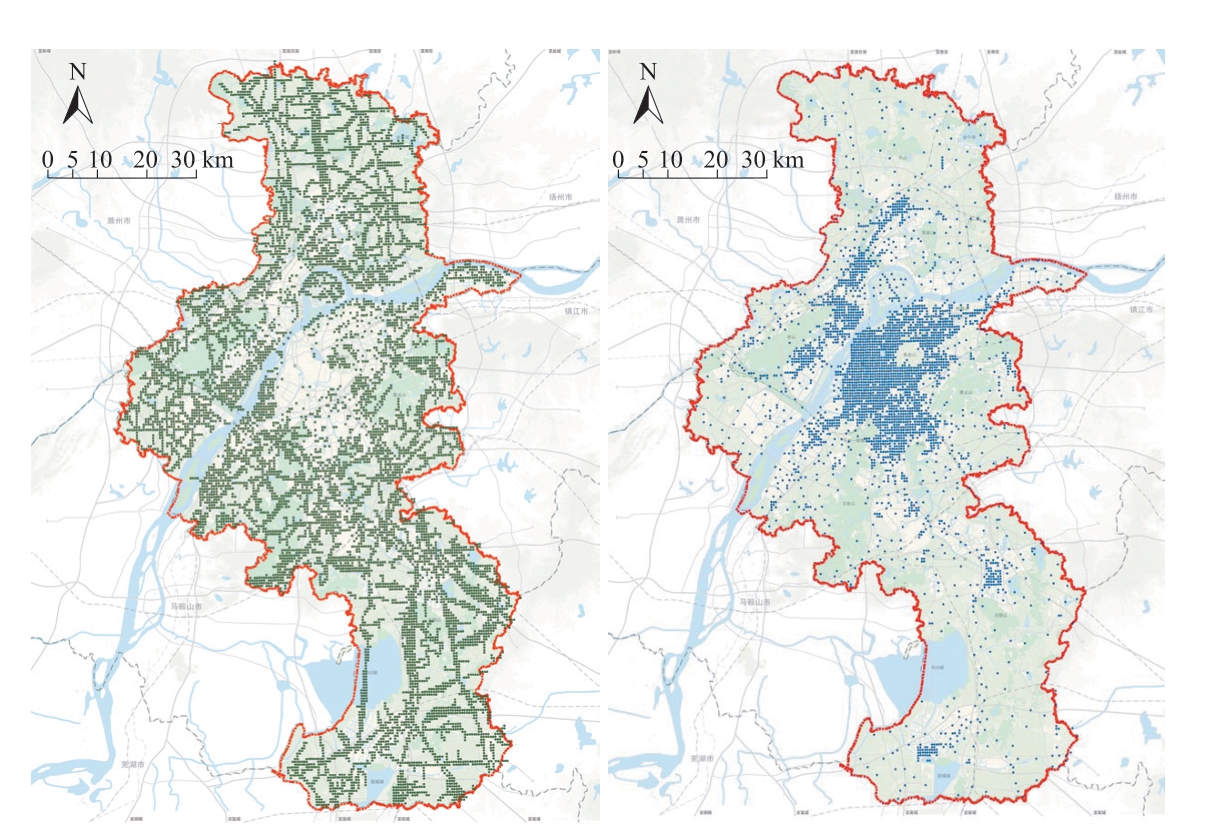
图4 分类训练数据集样本分布:分类区间0(左),分类区间1(右)
3 基于卷积神经网络模型的模型建构
本文的建模基本框架选用卷积神经网络模型中的深度残差模型,由三个步骤和六类模块构成(图5)。三个步骤分别为:数据输入、特征提取、结果输出。其中,特征提取部分运用多层卷积对已有特征进行计算提取,并通过连续的残差单元构建残差网络以加深深度;结果输出部分对人群随时间变化的24 维向量使用主成分分析进行降维与反变换处理,以节省计算时间。整体采用分批训练的方法对参数进行迭代更新,首先输入小批量的训练样本,经过多层卷积得到模拟结果,计算每批数据模拟结果与实际结果的误差,并将损失函数得分输入误差函数,再利用自适应矩估计(Adam)优化器进行反向求导以确定梯度向量,根据梯度向量来调整网络中的每一个参数,使误差收敛,实现超参数的优化。所有批次更新后,将验证集输入模型,得到模型在验证集上的模拟效果,再计算实际24 维结果与模拟24 维结果的均方根误差,该过程称为一次迭代。在后续迭代中,利用早停法(early stopping)确定迭代次数,取验证集历史最小均方根误差所对应的模型参数为最终结果。
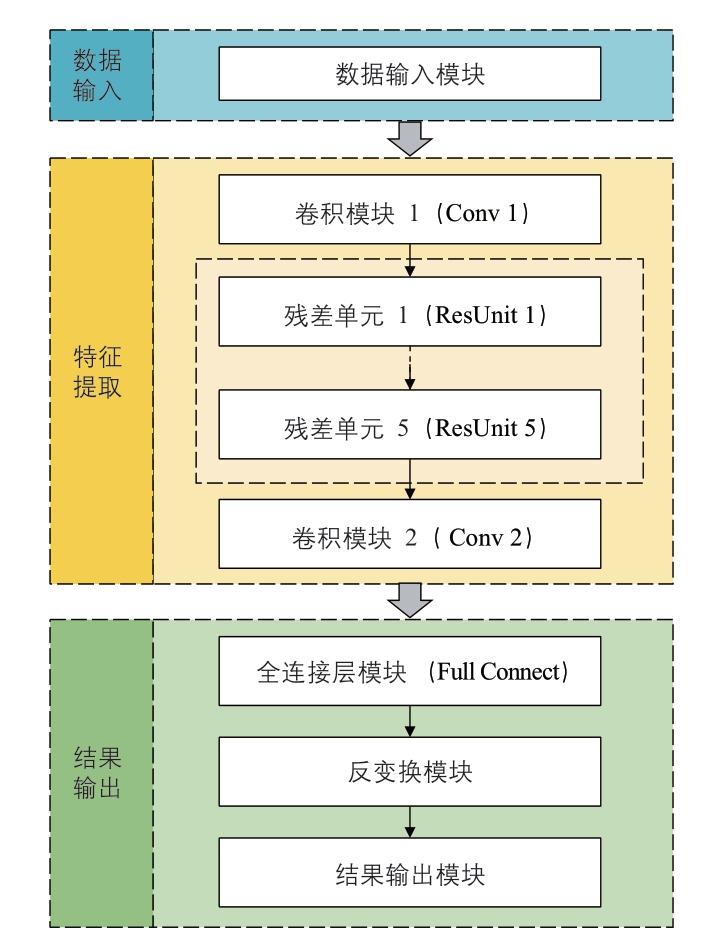
图5 模型构建框架示意图
将城市格栅数据按8∶1∶1 的比例划分为训练集、验证集、测试集三部分。训练集用于训练得到模型;验证集用于检验模型的训练程度以进行参数调整和模型选择;测试集用于检验模型的最终效果,评估模型的准确率、适用性和误差等。数据集的划分采用随机抽样的方法,避免过分集中或局部缺失。
4 模型评价与误差分析
4.1 模型评价
为了评价模型所采用的基于残差网络的卷积神经网络方法的科学性,使用多元线性回归算法、基于决策树的XGBoost 算法和不包含残差单元的卷积神经网络算法对数据集进行计算,并将结果进行对比(表3)。根据平均绝对误差(MAE)、均方根误差(NRMSE)和命中率(Precision-a)三项指标的计算结果,本研究所采用的基于残差网络的卷积神经网络模型具有更好的拟合精度。
表3 多种算法模拟结果评价指标对比
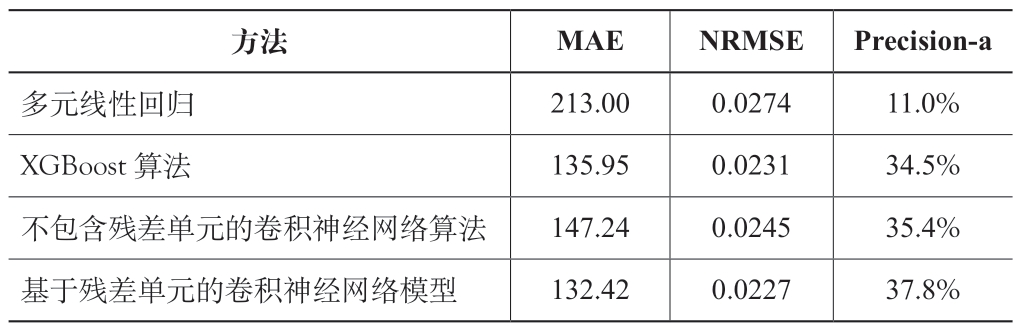
方法MAE NRMSE Precision-a多元线性回归213.00 0.0274 11.0%XGBoost 算法135.95 0.0231 34.5%不包含残差单元的卷积神经网络算法147.24 0.0245 35.4%基于残差单元的卷积神经网络模型132.42 0.0227 37.8%
4.2 误差分布分析
为更好地衡量模型的预测值与实际值的比例关系,本研究采用平均百分比误差(MAPE)评估模型的预测结果。观察平均百分比误差在各个人群密度区间的分布,发现MAPE随人群密度的增加呈现幂律分布(图6)。在空间分析单元的日时均人数超过800 人后,MAPE 稳定在30%以下。日时均人数在800 人以下的空间分析单元,平均百分比误差相对较高,这说明模型对人群密度较高的地块适应性更好。人群密度较低的地块虽然MAPE 较大,但由于人群密度基数较低,模型偏差的绝对值也较低。
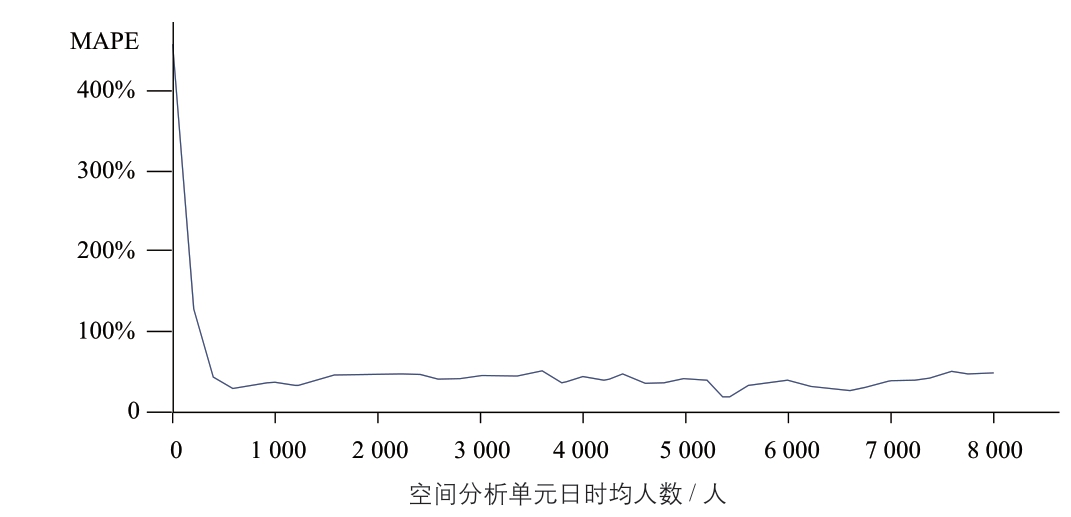
图6 平均百分比误差在各个人群密度区间的分布
对老城区、主城区、中心城区和市域四个空间圈层的MAPE 进行比较。老城内MAPE 在30%以内的空间分析单元占比达76.92%,模型拟合效果良好。而对于老城以外的空间分析单元,MAPE 随着主城—中心城区—市域圈层拓展而显著上升,说明模型拟合的准确性随城市圈层的拓展而降低(表4)。
表4 不同空间区域分段MAPE 分布占比表
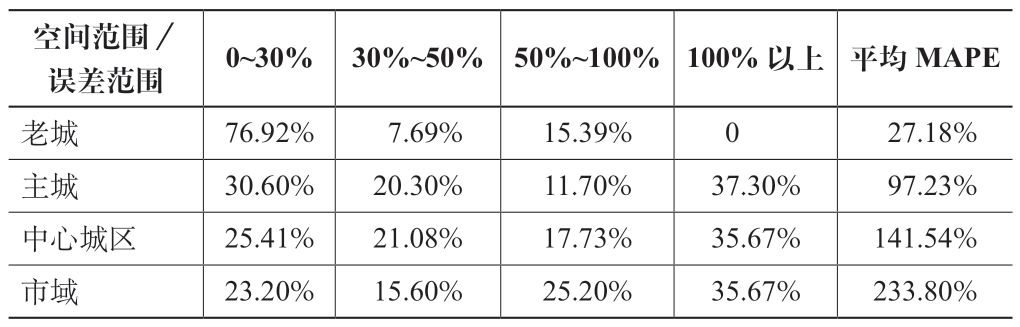
空间范围/误差范围0~30% 30%~50% 50%~100% 100%以上 平均MAPE老城76.92% 7.69%15.39%0 27.18%主城30.60%20.30%11.70%37.30% 97.23%中心城区25.41%21.08%17.73%35.67%141.54%市域23.20%15.60%25.20%35.67%233.80%
将MAPE 投影在城市空间,观察模型误差的空间分布规律。发现距离城市主中心5 km 内以老城为主的区域,90%以上的空间分析单元的MAPE 处于低值区间,模型拟合准确性最高;相较主城,江北副城、东山副城和仙林副城的误差更大(图7)。主城范围内,河西、城南、铁北三大片区的误差分布存在差异,河西片区从北至南拟合准确率显著递增(图8)。城南片区与铁北片区的空间误差分布不存在明显的准确性差异,拟合水平较高的空间分析单元分布更为均匀,拟合水平较低的空间分析单元多沿某条道路线性分布,如城南片区的花神大道沿线,铁北片区的红山路、恒嘉路沿线。

图7 平均百分比误差(MAPE)的空间分布(左:市域范围;右:主城区范围)
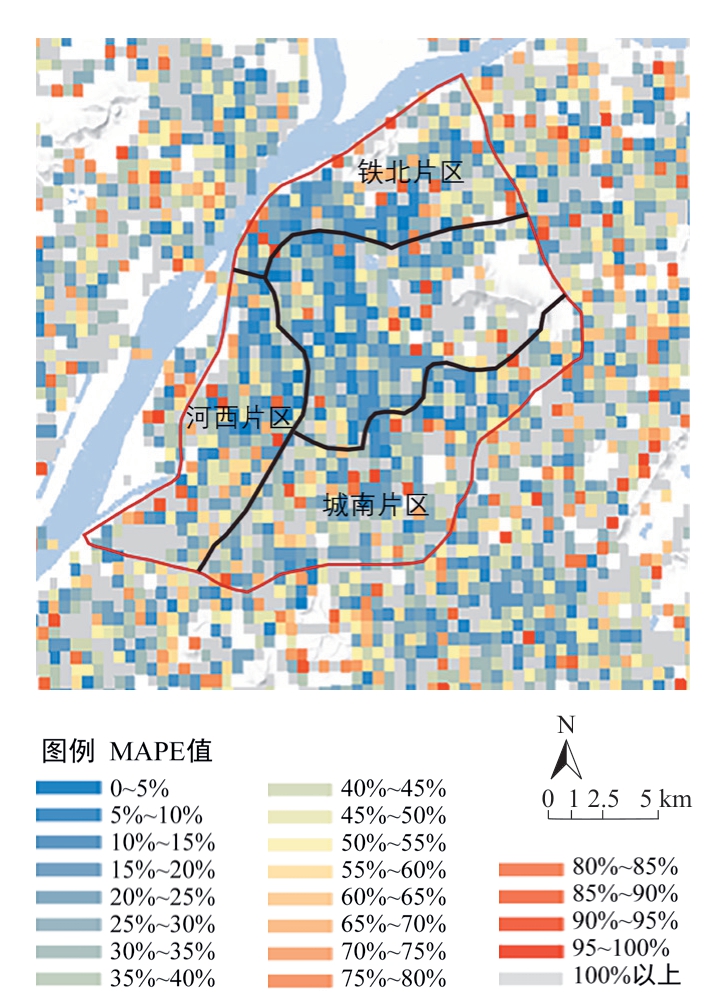
图8 主城区内各片区的平均百分比误差分布
将模型误差分布与南京城市各片区发展特点进行对比,发现准确性最高的片区主要是位于城市主中心5 km 以内的新街口等核心片区和城市远郊未集中建设区域;在中心城区外围的东山副城西部、河西北部副城、仙林副城西部等2000 年前后进行集中建设、现状发展较成熟的新城片区,模拟准确性较高;但处于城市近郊处拓展和建设中的建成区边缘的片区,模型存在较大误差。
从片区人群密度来看,模型对城市中心区域和城市远郊未集中建设区域的拟合度均较高,这两类区域在人群密度区间中分别对应人群高密度分布区域和低密度分布区域。但城市近郊处于拓展和建设中的建成区边缘的片区,人群密度还处于快速提升的中密度阶段,模型对该类片区的适应性较差。
4.3 建成环境要素与误差的相关性分析
笔者使用皮尔森相关性系数对模型中的建成环境因子特征值与MAPE 值进行相关性分析,讨论模型建成环境因素对模型误差的影响。发现空间容量、用地混合度、可达性与业态成熟度对模型准确性有正向影响,老城和主城区相比外围郊区在上述指标上占有优势,这印证了老城与主城区模型准确性较高的特点。从土地利用类型来看,以居住和公益性服务用地为主导的城市片区模拟准确性更高,而以商业商务和工业用地为主的城市片区模拟准确性较低,其他建成环境因素对模型准确性的相关性并不显著。
4.4 高误差片区聚类校验
将模型误差较高的片区根据建成环境特征进行聚类,获得六类特征区域,选取其中的典型空间分析单元,结合实地调研探讨误差原因。可以发现误差较高的片区主要为城市核心区或城市近郊区的开发强度较低或可达性较低的片区,并且大多高误差片区的土地利用类型为工业用地(表5)。
表5 高误差空间分析单元分类与典型空间分析单元汇总表

序号类别特征MAPEmax MAPEmin MAEmax MAEmin实际/模拟时空分布1城市核心区中开发强度较低、以居住功能为主、可达性较好的区域 2.43 0.042 2 067.5 13.70images/BZ_45_1893_530_2217_674.png2城市核心区和城市近郊的开发强度较低、以非建设用地为主、具有一定可达性的区域44.18 0.021 1 750.5 4.30images/BZ_45_1896_698_2214_845.png3城市核心区和城市近郊的开发强度较低、用地功能混合、具有一定可达性的区域27.16 0.033 2 201.2 5.65images/BZ_45_1894_868_2216_1013.png4城市核心区和城市近郊的以工业用地为主、可达性较高的区域85.34 0.028 2 371.9 2.49images/BZ_45_1893_1036_2217_1175.png5城市远郊的开发强度较低、可达性较低、以居住用地为主的区域51.74 0.014 2 960.3 2.56images/BZ_45_1894_1198_2216_1338.png6城市远郊的开发强度较低、可达性较低、以工业用地为主的区域40.08 0.012 1 101.2 8.62images/BZ_45_1895_1361_2215_1498.png真实预测
5 总结与讨论
本文首先利用卷积神经网络中的深度残差算法,架构了基于建成环境的人群时空分布预测模型,构建了以建成环境特征出发测算人群时空密度分布特征的方法;其次以南京为实证案例进行模型的训练和检验,对模型的准确性进行评价,并对模型误差的空间分布和影响误差的相关因子进行研究,产生了如下结论和引申讨论。
(1)采用包含残差单元的卷积神经网络算法进行人群时空分布预测模型建构,其效果优于统计回归算法和采用非图像特征的机器学习算法,相比不考虑残差单元的卷积神经网络算法也有优势。基于包含残差单元的卷积神经网络算法,能够为人群时空分布测算以及未来人群分布预测提供更为准确的数理模型。
(2)误差的空间分布显示人群时空分布预测模型准确性呈现“微笑曲线”。模型拟合准确性最高的区域分别为城市中心区域(人群密度高值区)和城市远郊未集中建设区域(人群密度低值区),城市近郊建成区的边缘片区的模型准确性较低。由于城市中心区域和城市远郊区域的开发建设状态稳定,建成环境特征也较为稳定和成熟,所以这两类片区人群活动也呈现出稳定的时空特征,表现为稳定的人群时空分布密度。而城市近郊建成区的边缘区处于城市快速拓展和建设状态,人群活动与空间开发往往尚未达成同步。在现实观察中,“卧城”“鬼城”等人群时空分布与城市建设缺乏协调的现象,也往往出现在城市拓展中的新城片区。后两类片区建成环境变化快,相关配套往往不成熟,人群活动受经济社会因素影响更大,因此导致模型产生了较大的拟合误差。未来模型优化需要加入入住率等反映城市片区居民活动稳定程度的指标。
(3)误差在不同功能片区的差异显示居住、公益性服务用地为主导的城市片区的模型准确性更高,而以工业用地、商业商务为主的城市片区模拟准确性较低。居住、公益性服务用地人群活动类型和活动时间规律相对较为稳定,而工业用地和商业商务的活动较为复杂,时间规律较弱,这些可能是导致不同类型用地的模型准确性存在差异的原因。因此,在今后的模型优化中,通过产业类型、生产方式等要素对工业用地、商业商务片区的活动内容进行进一步细分,有望提升模型的准确性。
(4)本文所采用人群分布数据是手机基站数据,城市郊区基站相对城市中心较为稀疏,可能会对本研究模型结果产生干扰,未来可以利用更高空间精度的时空数据对模型进行进一步的验证。
注:文中图表均为作者绘制。
[1] 徐东云, 张雷. 城市交通拥堵与城市化进程的关系初探[J]. 综合运输,2007(10): 12-16.
[2] 杜江, 刘渝. 城市化与环境污染:中国省际面板数据的实证研究[J]. 长江流域资源与环境, 2008, 17(6): 825-830.
[3] 陈海燕, 贾倍思. 紧凑还是分散?——对中国城市在加速城市化进程中发展方向的思考[J]. 城市规划, 2006, 30(5): 61-69.
[4] 张学勇. 我国大城市地区新城成长与主城共生策略研究[D]. 哈尔滨:哈尔滨工业大学, 2011.
[5] 席广亮, 甄峰. 智慧城市建设推动新型城镇化发展策略思考[J]. 上海城市规划, 2014(5): 26-29.
[6] CLARK C. Urban population densities[J]. Journal of Royal Statistics Society:series a, 1951, 114: 490-494.
[7] 毛汉英, 方创琳. 我国新一轮国土规划编制的基本构想[J]. 地理研究,2002, 21(3): 267-275.
[8] 兰宗敏, 冯健. 城中村流动人口日常活动时空间结构——基于北京若干典型城中村的调查[J]. 地理科学, 2012, 32(4): 409-417.
[9] 任常兴, 吴宗之, 刘茂. 城市公共场所人群拥挤踩踏事故分析[J]. 中国安全科学学报, 2005, 15(12): 102-106, 137.
[10] SANTA GUZMÁN L F. A statistical approach for studying urban human dynamics[D]. Lisbon: Universidade NOVA de Lisboa, 2018.
[11] HOTEIT S, SECCI S, SOBOLEVSKY S, et al. Estimating real human trajectories through mobile phone data[C] // 2013 IEEE 14th International Conference on Mobile Data Management, 2013: 148-153.
[12] BATTY M. The new science of cities[M]. Cambridge, MA: MIT Press, 2013.
[13] LUCA M, BARLACCHI G, LEPRI B, et al. Deep learning for human mobility: a survey on data and models[J]. arXiv: 2012.02825.
[14] LUCA M, BARLACCHI G, LEPRI B, et al. A survey on deep learning for human mobility[J]. ACM Computing Surveys (CSUR), 2021, 55(1): 1-44.
[15] QIAN W. Discovering human mobility from mobile data: probabilistic models and learning algorithms[D]. Besancon: Université Bourgogne Franche-Comté, 2020.
[16] 吴志强. 人工智能推演未来城市规划[J]. 经济导刊, 2020(1): 58-62.
[17] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[J]. Communications of the ACM,2012, 60: 84-90.